题目内容
抛物线y=x2-4x-4的顶点坐标是分析：本题可以运用配方法求顶点坐标，也可以根据顶点坐标公式求坐标．
解答：解：解法1：利用公式法y=ax2+bx+c的顶点坐标公式为（-
，
），
代入数值求得顶点坐标为（2，-8）；
解法2：利用配方法y=x2-4x-4=x2-4x+4-8=（x-2）2-8，
所以顶点的坐标是（2，-8）．
故答案为：（2，-8）．
| b |
| 2a |
| 4ac-b2 |
| 4a |
代入数值求得顶点坐标为（2，-8）；
解法2：利用配方法y=x2-4x-4=x2-4x+4-8=（x-2）2-8，
所以顶点的坐标是（2，-8）．
故答案为：（2，-8）．
点评：本题考查求抛物线的顶点坐标、对称轴的方法．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
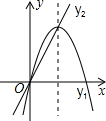如图，抛物线y1=-x2+4x和直线y2=2x．当y1＞y2时，x的取值范围是（ ）| A、0＜x＜2 | B、x＜0或x＞2 | C、x＜0或x＞4 | D、0＜x＜4 |