Question

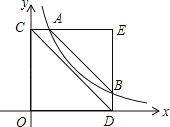
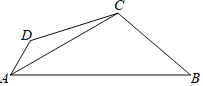
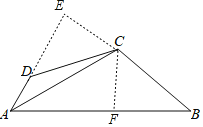
【题目】如图，已知四边形ABCD中，AC平分∠DAB，∠DAB＝60°，∠B与∠D互补，AC＝4，CD＝3，则AB﹣AD＝_____．

Answer 1

【答案】2．

【解析】

利用“截长补短”中的补短，补出邻补角即可出现相等角度，求出△DEC≌△BFC和△EAC≌△FAC，推出DE＝BF，AE＝AF，求出AB﹣AD＝2DE，求出DE即可．

解：过C作CE⊥AD交AD的延长线于E，CF⊥BA于F，则∠E＝∠CFB＝90°，

∵AC平分∠DAB，

∴CE＝CF，

∵∠B与∠ADC互补，

∴∠B+∠ADC＝180°，

∵∠ADC+∠EDC＝180°，

∴∠B＝∠EDC，

在△DEC和△BFC中

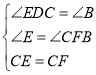
∴△DEC≌△BFC，

∴DE＝BF，

∵AC平分∠DAB，

∴∠EAC＝∠FAC＝

在△EAC和△FAC中

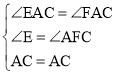
∴△EAC≌△FAC，

∴AE＝AF，

∴AB﹣AD＝（AF+BF）﹣（AE﹣DE）＝（AE+DE）﹣（AE﹣DE）＝2DE，

∵在Rt△AEC中，∠E＝90°，∠EAC＝30°，AC＝4，

∴CE＝AC＝2，

在Rt△DEC中，∠E＝90°，DC＝3，CE＝2，

由勾股定理得：DE＝＝＝，

∴AB﹣AD＝2DE＝2，

故答案为：．