题目内容
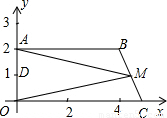
在梯形ABCO中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别是A(8,0),B(8,10),C(0,4).点D(4,7)为线段BC的中点,动点P从O点出发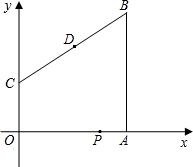 ,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.
,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.
(1)求直线BC的解析式;
(2)设△OPD的面积为s,求出s与t的函数关系式,并指出自变量t的取值范围;
(3)当t为何值时,△OPD的面积是梯形OABC的面积的 ?
?
解:(1)设直线BC的解析式为y=kx+b,
将C(0,4),B(8,10)代入得:
 ,
,
解得: ,
,
即y= x+4,
x+4,
所以直线BC的解析式为:y= x+4.
x+4.
(2)有两种情况:
①当P在OA上运动时;
∴OP=t×1=t,△OPD的边OP上的高是7,
∴△OPD的面积为:
S= ×t×7
×t×7
即S= t(0<t≤8),
t(0<t≤8),
②当P在AB上运动时:
∵A(8,0),B(8,10),C(0,4),D(4,7),
△ODC的面积为:
S1= ×4×4=8,
×4×4=8,
△OPA的面积是:
S2= ×8×(t-8)=4t-32,
×8×(t-8)=4t-32,
△DBP的面积是:
S3= ×{10-(t-8)}×(8-4)=36-2t,
×{10-(t-8)}×(8-4)=36-2t,
四边形OABC的面积是:
S4= ×(4+10)×8=56,
×(4+10)×8=56,
∴△ODP的面积是:
S=S4-S1-S2-S3=56-8-(4t-32)-(36-2t)=-2t+44,
即S=-2t+44(8<t≤18),
∴S= ;
;

(3)由(2)可知:
a: t=
t= ×56,
×56,
解得t=6秒,
b:-2t+44= ×56,
×56,
解得t=11.5秒,
∴t=6秒或t=11.5秒.
分析:用待定系数法设出直线BC的解析式为Y=kx+b,代入求出一次函数的解析式是y= x+4,再用面积公式s=
x+4,再用面积公式s= ab求出P的坐标,进一步求出s与t的关系式
ab求出P的坐标,进一步求出s与t的关系式
点评:这题的关键是考查已知两点坐标用设出解析式y=kx+b求出一次函数的解析式,利用面积公式求出关系式,利用分类讨论思想求出t值.
将C(0,4),B(8,10)代入得:
 ,
,解得:
 ,
,即y=
 x+4,
x+4,所以直线BC的解析式为:y=
 x+4.
x+4.(2)有两种情况:
①当P在OA上运动时;
∴OP=t×1=t,△OPD的边OP上的高是7,
∴△OPD的面积为:
S=
 ×t×7
×t×7即S=
 t(0<t≤8),
t(0<t≤8),②当P在AB上运动时:
∵A(8,0),B(8,10),C(0,4),D(4,7),

△ODC的面积为:
S1=
 ×4×4=8,
×4×4=8,△OPA的面积是:
S2=
 ×8×(t-8)=4t-32,
×8×(t-8)=4t-32,△DBP的面积是:
S3=
 ×{10-(t-8)}×(8-4)=36-2t,
×{10-(t-8)}×(8-4)=36-2t,四边形OABC的面积是:
S4=
 ×(4+10)×8=56,
×(4+10)×8=56,∴△ODP的面积是:
S=S4-S1-S2-S3=56-8-(4t-32)-(36-2t)=-2t+44,
即S=-2t+44(8<t≤18),
∴S=
 ;
;
(3)由(2)可知:
a:
 t=
t= ×56,
×56,解得t=6秒,
b:-2t+44=
 ×56,
×56,解得t=11.5秒,
∴t=6秒或t=11.5秒.
分析:用待定系数法设出直线BC的解析式为Y=kx+b,代入求出一次函数的解析式是y=
 x+4,再用面积公式s=
x+4,再用面积公式s= ab求出P的坐标,进一步求出s与t的关系式
ab求出P的坐标,进一步求出s与t的关系式点评:这题的关键是考查已知两点坐标用设出解析式y=kx+b求出一次函数的解析式,利用面积公式求出关系式,利用分类讨论思想求出t值.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
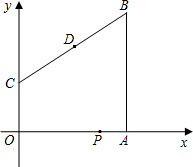 ,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.
,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.