题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:因为AB∥x轴,BC∥y轴,而AD∥BC,CD∥AB,所以点D的横坐标与点A的横坐标相同,纵坐标与点C的纵坐标相同,所以点D的坐标为(2, |
(2) |
解:因为AB=5-2=3,AD= |
(3) |
解:将这个四边形向下平移 解题指导:解答有关直角坐标系中图形的问题时,弄清点的坐标的几何意义非常重要,其中点的横坐标的绝对值表示这个点到y轴的距离,纵坐标的绝对值表示到x轴的距离. |

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目

 如图所示,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
如图所示,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….

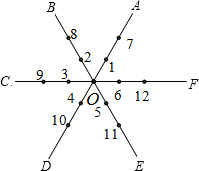 如图所示,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
如图所示,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….