题目内容
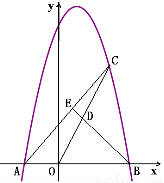
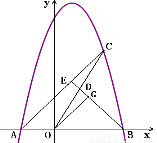
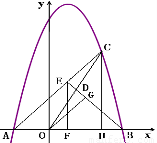
如图,已知抛物线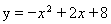 与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
(1)说明: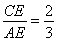 ;
;
(2)当点C、点A到y轴距离相等时,求点E坐标.
(3)当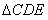 的面积为
的面积为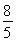 时,求
时,求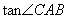 的值.
的值.
(1)理由见解析;(2)(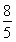 ,
,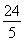 );(3)2.
);(3)2.
【解析】
试题分析:(1)由y=0,得出的一元二次方程的解就是A、B两点的横坐标.由此可求出A、B的坐标。通过构建相似三角形求解,过O作OG∥AC交BE于G,那么可得出两组相似三角形:△GED∽△OGD、△BOG∽△BAE,可分别用这两组相似三角形得出OG与EC的比例关系、OG与AE的比例关系,从而得出CE、AE的比例关系.
(2)由已知可求C(2,8),再求AC所在直线解析式,根据△AEF∽△ACH可求E点坐标.
(3)由D是OC的中点可知S△OCE=2S△CDE,又由已知可求S△AOC=8,从而可求出CH、AH的值,从而可求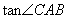 的值.
的值.
试题解析:(1)令y=0,则有-x2+2x+8=0.
解得:x1=-2,x2=4
∴OA=2,OB=4.
过点O作OG∥AC交BE于G
∴△CEG∽△OGD
∴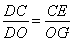
∵DC=DO
∴CE=0G
∵OG∥AC
∴△BOG∽△BAE
∴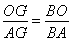
∵OB=4,OA=2
∴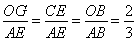 ;
;
(2)由(1)知A(-2,0),且点C、点A到y轴的距离相等,
∴C(2,8)
设AC所在直线解析式为:y=kx+b
把 A 、C两点坐标代入求得k=2,b=4
所以y=2x+4
分别过E、C作EF⊥x轴,CH⊥x轴,垂足分别为F、H
由△AEF∽△ACH可求EF=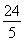 ,OF=
,OF=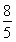 ,
,
∴E点坐标为(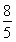 ,
,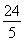 )
)
(3)连接OE
∵D是OC的中点,
∴S△OCE=2S△CED
∵S△OCE: S△AOC=CE:CA=2:5
∴S△CED:S△AOC=1:5.
∴S△AOC=5S△CED=8
∴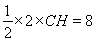
∴CH=8
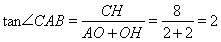
考点: 二次函数综合题.

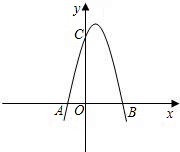 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).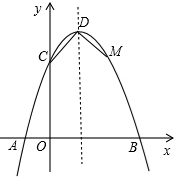 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1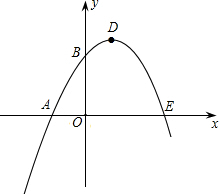 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )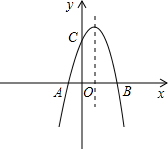 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).