题目内容
 如图,⊙A与⊙B外切于点P,它们的半径分别为6和2,直线CD与它们都相切,切点分别为C,D,则图中阴影部分的面积是( )
如图,⊙A与⊙B外切于点P,它们的半径分别为6和2,直线CD与它们都相切,切点分别为C,D,则图中阴影部分的面积是( )A、16
| ||||
B、16
| ||||
C、16
| ||||
D、16
|
分析:要求阴影部分的面积,就要明确阴影部分的面积=梯形ABDC的面积-扇形ACP的面积-扇形BPD的面积,然后根据面积公式分别计算即可.
解答: 解:连接AC,BD,AB,过点B作BE⊥AC,
解:连接AC,BD,AB,过点B作BE⊥AC,
所以BE=
=4
,
∵AB=PA+PB=8,
∴sin∠A=
=
,
∴∠A=60°,
∴∠ABE=30°,
∴∠ABD=120°,
梯形ABDC的面积是:
(6+2)•4
=16
;
扇形ACP的面积为
;
扇形BPD的面积为
;
则图中阴影部分的面积=梯形ABDC的面积-扇形ACP的面积-扇形BPD的面积=16
-
π.
故选D.
 解:连接AC,BD,AB,过点B作BE⊥AC,
解:连接AC,BD,AB,过点B作BE⊥AC,所以BE=
| 64-16 |
| 3 |
∵AB=PA+PB=8,
∴sin∠A=
| BE |
| AB |
| ||
| 2 |
∴∠A=60°,
∴∠ABE=30°,
∴∠ABD=120°,
梯形ABDC的面积是:
| 1 |
| 2 |
| 3 |
| 3 |
扇形ACP的面积为
| 60π•36 |
| 360 |
扇形BPD的面积为
| 120π•4 |
| 360 |
则图中阴影部分的面积=梯形ABDC的面积-扇形ACP的面积-扇形BPD的面积=16
| 3 |
| 22 |
| 3 |
故选D.
点评:本题涉及的知识点比较多.要掌握的是:切线的性质,圆与圆的位置关系,扇形的面积公式以及直角三角形的性质.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 37、如图,⊙O1与⊙O2外切于点C,一条外公切线切两圆于点A,B,已知⊙O1的半径是9,⊙O2的半径是3,求∠BAC的度数.
37、如图,⊙O1与⊙O2外切于点C,一条外公切线切两圆于点A,B,已知⊙O1的半径是9,⊙O2的半径是3,求∠BAC的度数.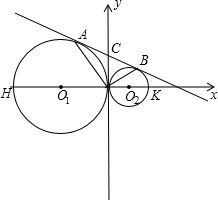 DNC是矩形?
DNC是矩形?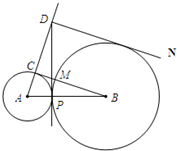 22、已知:如图,⊙A与⊙B外切于点P,BC切⊙A于点C,⊙A与⊙B的内公切线PD交AC于点D,交BC于点M.
22、已知:如图,⊙A与⊙B外切于点P,BC切⊙A于点C,⊙A与⊙B的内公切线PD交AC于点D,交BC于点M. (2012•淮安)如图,⊙M与⊙N外切,MN=10cm,若⊙M的半径为6cm,则⊙N的半径为
(2012•淮安)如图,⊙M与⊙N外切,MN=10cm,若⊙M的半径为6cm,则⊙N的半径为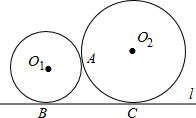 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.