Question

（2013•威海）如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°，反比例函数y1=

m

x

的图象经过点A，反比例函数y2=

n

x

的图象经过点B，则下列关于m，n的关系正确的是（　　）

• A．m=-3n
• B．m=-

  3

  n
• C．m=-

  3

  3

  n
• D．m=

  3

  3

  n

Answer 1

分析：过点B作BE⊥x轴于点E，过点A作AF⊥x轴于点F，设点B坐标为（a，

n

a

），点A的坐标为（b，

m

b

），证明△BOE∽△OAF，利用对应边成比例可求出m、n的关系．

解答：解：过点B作BE⊥x轴于点E，过点A作AF⊥x轴于点F，

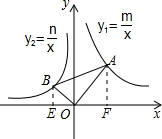
设点B坐标为（a，

n

a

），点A的坐标为（b，

m

b

），
∵∠OAB=30°，
∴OA=

3

OB，
设点B坐标为（a，

n

a

），点A的坐标为（b，

m

b

），
则OE=-a，BE=

n

a

，OF=b，AF=

m

b

，
∵∠BOE+∠OBE=90°，∠AOF+∠BOE=90°，
∴∠OBE=∠AOF，
又∵∠BEO=∠OFA=90°，
∴△BOE∽△OAF，
∴

OE

AF

=

BE

OF

=

OB

AO

，即

-a

m b

=

n a

b

=

1

3

，
解得：m=-

3

ab，n=

ab

3

，
故可得：m=-3n．
故选A．

点评：本题考查了反比例函数的综合，解答本题的关键是结合解析式设出点A、B的坐标，得出OE、BE、OF、AF的长度表达式，利用相似三角形的性质建立m、n之间的关系式，难度较大．