Question

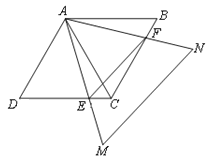
【题目】如图，△ABC、△ADC、△AMN均为等边三角形，AM＞AB，AM与DC交于点E，AN与BC交于点F.

(1)试说明：△ABF≌△ACE；

(2)猜测△AEF的形状，并说明你的结论；

(3)请直接指出当F点在BC何处时，AC⊥EF.

Answer 1

【答案】(1)证明见解析；（2）△AEF为等边三角形，证明见解析；（3）当点F为BC中点时，AC⊥EF.

【解析】

（1）由已知条件易得AB=AC，∠B=∠BAC =∠MAN=∠ACD=60°，进而可得∠BAF=∠CAE，由此即可证得△ACE≌△ABF；

（2）由（1）中所得△ACE≌△ABF可得AE=AF，结合∠MAN=60°即可得到△AEF是等边三角形；

（3）当点F为BC中点时，根据“等腰三角形的三线合一”可得∠CAF=∠BAF=30°，结合∠EAF=60°可得∠CAE=∠CAF=30°，结合AE=AF即可得到此时AC⊥EF.

(1)∵△ABC、△ADC均为等边三角形，

∴AB=AC，∠B=∠BAC =∠DAC=∠ACD=60°

∴∠BAC－∠FAC=∠MAN－∠FAC，即∠BAF=∠CAE ，

∴△ACE≌△ABF（AAS）；

（2）△AEF为等边三角形，

∵△ACE≌△ABF，

∴AE=AF，

∵△AMN为等边三角形，

∴∠MAN=60°，

∴△AEF为等边三角形；

（3）当点F为BC中点时，AC⊥EF ，理由如下：

∵点F是BC的中点，△ABC是等边三角形，

∴AF平分∠BAC，∠BAC=60°，

∴∠FAC=30°，

又∵△AEF是等边三角形，

∴∠EAF=60°，

∴∠EAC=∠AEF-∠FAC=30°，

∴此时，AC平分∠EAF，

又∵△AEF是等边三角形，

∴AC⊥EF.