Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ≥§∑Ĺ–ő![]() ÷–£¨
÷–£¨![]() £¨Ķ„
£¨Ķ„![]() ļÕĶ„
ļÕĶ„![]() ∂ľ «ī”
∂ľ «ī”![]() Ķ„≥Ų∑Ę£¨Ķ„
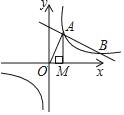
Ķ„≥Ų∑Ę£¨Ķ„![]() ‘ŕ’‚łŲ≥§∑Ĺ–őĶńĪŖ…Ōň≥ Ī’Ž‘ň∂Į£¨Ķ„
‘ŕ’‚łŲ≥§∑Ĺ–őĶńĪŖ…Ōň≥ Ī’Ž‘ň∂Į£¨Ķ„![]() ‘ŕ’‚łŲ≥§∑Ĺ–őĶńĪŖ…Ōńś Ī’Ž‘ň∂Į£¨ňŁ√«ĶńňŔ∂»∂ľ «√Ņ√Ž1łŲĶ•őĽ£¨…ŤňŁ√«Ķń‘ň∂Į Īľš «
‘ŕ’‚łŲ≥§∑Ĺ–őĶńĪŖ…Ōńś Ī’Ž‘ň∂Į£¨ňŁ√«ĶńňŔ∂»∂ľ «√Ņ√Ž1łŲĶ•őĽ£¨…ŤňŁ√«Ķń‘ň∂Į Īľš «![]() √Ž
√Ž![]()
£®1£©![]() Ī£¨«ůŌŖ∂ő
Ī£¨«ůŌŖ∂ő![]() Ķń≥§£Ľ
Ķń≥§£Ľ
£®2£©‘ŕ![]() ‘ň∂ĮĻż≥Ő÷–£¨Ń¨Ĺ”
‘ň∂ĮĻż≥Ő÷–£¨Ń¨Ĺ”![]() £¨…ŤŌŖ∂ő
£¨…ŤŌŖ∂ő![]() ļÕĶ„
ļÕĶ„![]() ňýĺ≠ĻżĶń¬∑ŌŖňý◊ť≥…Ķń∑‚Ī’ĶńÕľ–ő√śĽż «
ňýĺ≠ĻżĶń¬∑ŌŖňý◊ť≥…Ķń∑‚Ī’ĶńÕľ–ő√śĽż «![]() £¨«ů≥Ų
£¨«ů≥Ų![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę◊Ę√ų
ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę◊Ę√ų![]() Ķń»°÷Ķ∑∂őߣģ
Ķń»°÷Ķ∑∂őߣģ
£®3£©‘ŕ…Ō“Ľő ÷–£¨ «∑Ůīś‘ŕń≥łŲ ĪŅŐ![]() £¨ ĻĶ√
£¨ ĻĶ√![]() «≥§∑Ĺ–ő
«≥§∑Ĺ–ő![]() √śĽżĶń“ĽįŽ£Ņ»Űīś‘ŕ£¨«ů≥Ų
√śĽżĶń“ĽįŽ£Ņ»Űīś‘ŕ£¨«ů≥Ų![]() £Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£®4£©ĶĪ![]() Ķ„‘ŕ
Ķ„‘ŕ![]() …Ō‘ň∂Į Ī£®≤ĽįŁņ®Ķ„
…Ō‘ň∂Į Ī£®≤ĽįŁņ®Ķ„![]() £©£¨īś≤Ľīś‘ŕń≥“Ľ ĪŅŐ
£©£¨īś≤Ľīś‘ŕń≥“Ľ ĪŅŐ![]() £¨ ĻĶ√
£¨ ĻĶ√![]() «÷ĪĹ«»żĹ«–ő¬ū£Ņ»Űīś‘ŕ£¨«ů≥Ų
«÷ĪĹ«»żĹ«–ő¬ū£Ņ»Űīś‘ŕ£¨«ů≥Ų![]() £Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
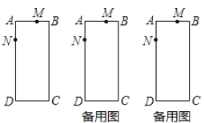
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©
£Ľ£®2£©![]() £¨
£¨![]() £Ľ£®3£©īś‘ŕ£¨
£Ľ£®3£©īś‘ŕ£¨![]() £Ľ£®4£©īś‘ŕ£¨
£Ľ£®4£©īś‘ŕ£¨![]()
°ĺĹ‚őŲ°Ņ
£®1£©«ů≥ŲAM£¨AN£¨ņŻ”√ĻīĻ…∂®ņŪ«ůĹ‚ľīŅ…£ģ
£®2£©∑÷ŃĹ÷÷«ť–ő£ļĶĪ0£ľt°‹4 Ī£¨ĶĪ4£ľt£ľ10 Ī£¨∑÷Īū«ůĹ‚ľīŅ…£ģ
£®3£©łýĺ›∑Ĺ≥ŐĹ‚ĺŲő Ő‚ľīŅ…£ģ
£®4£©ĻŘ≤žÕľŌůŅ…÷™£¨°ŌMAN£¨°ŌANM≤ĽŅ…ń‹ «÷ĪĹ«£ģĶĪ°ŌAMN=90°„ Ī£¨łýĺ›AN2=AM2+MN2£¨ĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£ģ
Ĺ‚£ļ£®1£©ĶĪt=3 Ī£¨AM=3£¨AN=3£¨
‘ŕRt°ųANM÷–£¨°Ŗ°ŌMAN=90°„£¨
°ŗ![]() £Ľ
£Ľ
£®2£©ĶĪ0£ľt°‹4 Ī£¨![]() £ģ
£ģ
ĶĪ4£ľt£ľ10 Ī£¨
![]() £Ľ
£Ľ
°ŗ![]()
£®3£©ĘŔ»ŰĶ„![]() ‘ŕ
‘ŕ![]() ∂ő£¨ľī
∂ő£¨ľī![]() £¨
£¨![]()
°ŗ![]() £¨
£¨
ľī![]() £¨
£¨
Ĺ‚Ķ√£ļ![]() £®…Š»•£©£Ľ
£®…Š»•£©£Ľ
Ęŕ»ŰĶ„![]() ‘ŕ
‘ŕ![]() ŌŖ∂ő£¨ľī
ŌŖ∂ő£¨ľī![]() £ģ
£ģ
![]() £¨
£¨
ľī![]() £¨
£¨
Ĺ‚Ķ√£ļ![]() £Ľ
£Ľ
£®4£©ĶĪĶ„![]() ‘ŕ
‘ŕ![]() …Ō‘ň∂Į Ī£¨°ŌMAN£¨°ŌANM≤ĽŅ…ń‹ «÷ĪĹ«£ģ
…Ō‘ň∂Į Ī£¨°ŌMAN£¨°ŌANM≤ĽŅ…ń‹ «÷ĪĹ«£ģ
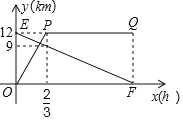
ĶĪ![]() Ī£¨»ÁÕľ£ļĻżM◊ųMG°ÕAN£¨
Ī£¨»ÁÕľ£ļĻżM◊ųMG°ÕAN£¨
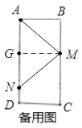
°ŗ![]()
”…Ő‚“‚÷™£¨![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £Ľ
£Ľ
°ŗ¬ķ◊„ŐűľĢĶńtĶń÷Ķő™8£ģ

 ľ‚◊”…ķ–¬ŅőŐ√Ņő Ī◊ų“ĶŌĶŃ–īūįł
ľ‚◊”…ķ–¬ŅőŐ√Ņő Ī◊ų“ĶŌĶŃ–īūįł ”Ę≤Ňľ∆ĽģÕ¨≤ĹŅő ĪłŖ–ß—ĶŃ∑ŌĶŃ–īūįł
”Ę≤Ňľ∆ĽģÕ¨≤ĹŅő ĪłŖ–ß—ĶŃ∑ŌĶŃ–īūįł