题目内容
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB= ,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
 ,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
(1)求直线BC的解析式;
(2)求经过B,C,A三点的抛物线y=ax2+bx+c的解析式;若抛物线的顶点为M,试判断点M是否在直线BC上,并说明理由。
(2)求经过B,C,A三点的抛物线y=ax2+bx+c的解析式;若抛物线的顶点为M,试判断点M是否在直线BC上,并说明理由。
解:(1)∵ ,
,
∴在Rt△COB中,OC=OB·tan30°= ,
,
∴点C的坐标我(1,0),
又点B的坐标为(0, ),
),
∴设直线BC的解析式为y=kx+ ,
,
∴0=k+ ,
,
∴k=- ,
,
则直线BC的解析式为: ;
;
(2)∵在Rt△AOB中, ,
,
∴A(3,0),
又 ,
,
∴ ,
,
解之得: ,
,
∴所求抛物线的解析式为 ,
,
配方得: ,
,
∴顶点为 ,
,
把x=2代入 ,得
,得 ,
,
∴顶点M不在直线BC上。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
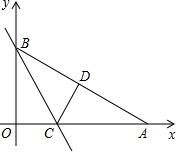 如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=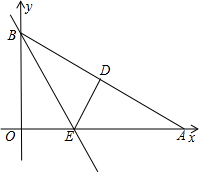 痕为BE.
痕为BE.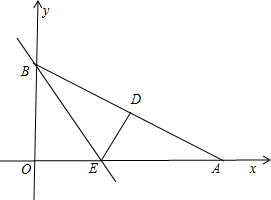 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上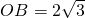 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折 痕为BE.
痕为BE.