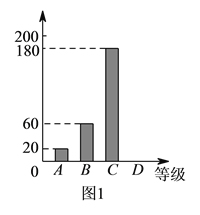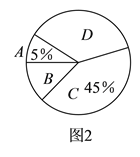题目内容
【题目】如图，直线y=mx与双曲线y=
相交于A、B两点，A点的坐标为（1，2），AC⊥x轴于C，连结BC．
（1）求反比例函数的表达式；
（2）根据图象直接写出当mx＞
时，x的取值范围；
（3）在平面内是否存在一点D，使四边形ABDC为平行四边形？若存在，请求出点D坐标；若不存在，请说明理由．
【答案】(1)、y=
；(2)、﹣1＜x＜0或x＞1；(3)、（﹣1，﹣4）
【解析】试题分析：(1)、将点A代入反比例函数解析式得出答案；(2)、根据图像得出答案；(3)、根据平行四边形的性质得出点D的坐标.
试题解析：(1)、把A（1，2）代入y=mx得m=2，则解析式是y=2x，
把A（1，2）代入y=
得：k=2，则解析式是y=
；
(2)、根据图象可得：﹣1＜x＜0或x＞1．
(3)、存在 D的坐标（﹣1，﹣4）
练习册系列答案
相关题目
【题目】今年入冬以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点，某校学生会为了调查学生对雾霾天气知识的了解程度，随机抽取了该校的若干名学生进行调查，将调查结果分为四个等级：（
）非常了解，（ 
）比较了解，（ 
）很少了解，（ 
）不了解，并将调查结果绘制成如下两幅不完整的统计图．
对雾霾天气了解程度的条形统计图 | 对雾霾天气了解程度的扇形统计图 |
|
|
根据统计图提供的信息，解答下列问题：
（
）求被调查的学生人数；并将条形统计图补充完整．
（
）本次调查结果的“众数”是__________．
（
）若该校有
名学生，请你估计该校对雾霾天气知识“不了解”的学生人数，并请你用一句话告诉这些学生有关雾霾的知识．
