题目内容
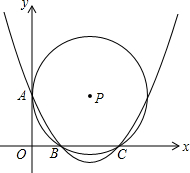 已知:如图,在平面直角坐标系xOy中,以点P(2,
已知:如图,在平面直角坐标系xOy中,以点P(2, )为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).
)为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).
(1)求经过A、B、C三点的抛物线的解析式;
(2)在(1)中的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 .如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;
.如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;
(3)如果一个动点D自点P出发,先到达y轴上的某点,再到达x轴上某点,最后运动到(1)中抛物线的顶点Q处,求使点D运动的总路径最短的路径的长.
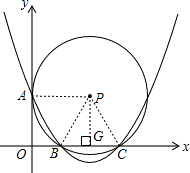 解:(1)连接PA,PB,PC,过点P作PG⊥BC于点G,
解:(1)连接PA,PB,PC,过点P作PG⊥BC于点G,∵⊙P与y轴相切于点A,
∴PA⊥y轴,
∵P(2,
 ),
),∴OG=AP=2,PG=OA=
 ,
,∴PB=PC=2,
∴BG=1,
∴CG=1,BC=2.
∴OB=1,OC=3.
∴A(0,
 ),B(1,0),C(3,0),
),B(1,0),C(3,0),根据题意设二次函数解析式为:y=a(x-1)(x-3),
则
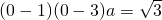 ,
,解得:a=
 .
.故二次函数的解析式为:
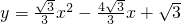 .
.(2)∵点B(1,0),点P(2,
 ),
),∴BP的解析式为:y=
 x-
x- ;
;则过点A平行于BP的直线解析式为:y=
 x+
x+ ,过点C平行于BP的直线解析式为:y=
,过点C平行于BP的直线解析式为:y= x-3
x-3 l2,
l2,从而可得①:
 x+
x+ =
= x2-
x2- x+
x+ ,
,解得:x1=0,x2=7,
从而可得满足题意的点M的坐标为(0,
 )、(7,8
)、(7,8 );
);②
 x-3
x-3 =
= x2-
x2- x+
x+ ,
,解得:x1=3,x2=4,
从而可得满足题意的点M的坐标为:(3,0)、(4,
 )
)综上可得点M的坐标为(0,
 ),(3,0),(4,
),(3,0),(4, ),(7,
),(7, ).
).(3)∵
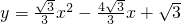 =
= ,
,∴抛物线的顶点Q(2,
 ).
).作点P关于y轴的对称点P',则P'(-2,
 ).
).连接P'Q,则P'Q是最短总路径,根据勾股定理,可得P'Q=
 .
.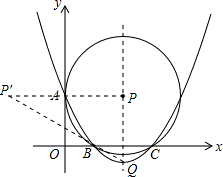 .
.分析:(1)连接PA,PB,PC,过点P作PG⊥BC于点G,求出P点的坐标,然后求得点A、B、C的坐标用待定系数法求得二次函数的解析式即可;
(2)因为△ABP和△CBP的面积是菱形ABCP面积的
 ,故过点A、C作BP的平行线,与抛物线的交点即是满足条件的点M.
,故过点A、C作BP的平行线,与抛物线的交点即是满足条件的点M.(3)将原方程配方后得到抛物线的顶点Q(2,
 ),然后作点P关于y轴的对称点P',则P’(-2,
),然后作点P关于y轴的对称点P',则P’(-2, ).连接P'Q,则P'Q是最短总路径,根据勾股定理,可得P′Q=
).连接P'Q,则P'Q是最短总路径,根据勾股定理,可得P′Q= .
.点评:此题考查了二次函数综合题,涉及了待定系数法求函数解析式、轴对称最短路径、菱形的性质,难点在第二问,关键是利用平行线的性质得出点M的寻找办法,难度较大.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

