ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ ![]() жаЃЌвбжЊ
жаЃЌвбжЊ ![]() ЃЌ
ЃЌ ![]() СНЕуЕФзјБъЗжБ№ЮЊ
СНЕуЕФзјБъЗжБ№ЮЊ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ ![]() ЩЯвЛЕуЃЈгы
ЩЯвЛЕуЃЈгы ![]() ЃЌ
ЃЌ ![]() ЕуВЛжиКЯЃЉЃЌХзЮяЯп
ЕуВЛжиКЯЃЉЃЌХзЮяЯп ![]()
![]() ЃЈ
ЃЈ ![]() ЃЉОЙ§Еу
ЃЉОЙ§Еу ![]() ЃЌ
ЃЌ ![]() ЃЌЖЅЕуЮЊ
ЃЌЖЅЕуЮЊ ![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп ![]()
![]() ЃЈ
ЃЈ ![]() ЃЉОЙ§Еу
ЃЉОЙ§Еу ![]() ЃЌ
ЃЌ ![]() ЃЌЖЅЕуЮЊ
ЃЌЖЅЕуЮЊ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФбгГЄЯпЯрНЛгкЕу
ЕФбгГЄЯпЯрНЛгкЕу ![]() ЃЎ
ЃЎ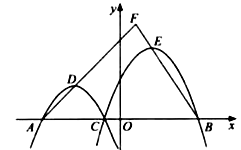
ЃЈ1ЃЉШє ![]() ЃЌ
ЃЌ ![]() ЃЌЧѓХзЮяЯп
ЃЌЧѓХзЮяЯп ![]() ЃЌ
ЃЌ ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШє ![]() ЃЌ
ЃЌ ![]() ЃЌЧѓ
ЃЌЧѓ ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЪЧЗёДцдкетбљЕФЪЕЪ§ ![]() ЃЈ
ЃЈ ![]() ЃЉЃЌЮоТл
ЃЉЃЌЮоТл ![]() ШЁКЮжЕЃЌжБЯп
ШЁКЮжЕЃЌжБЯп ![]() гы
гы ![]() ЖМВЛПЩФмЛЅЯрДЙжБЃПШєДцдкЃЌЧыжБНгаДГі
ЖМВЛПЩФмЛЅЯрДЙжБЃПШєДцдкЃЌЧыжБНгаДГі ![]() ЕФСНИіВЛЭЌЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФСНИіВЛЭЌЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКвРЬтПЩЕУЃК
НтЕУ ЃК
ЫљвдХзЮяЯпL1ЕФНтЮіЪНЮЊy=-![]() x2-
x2-![]() x-2.
x-2.
ЭЌРэЃЌ
НтЕУ ЃК
ЫљвдХзЮяЯпL2ЕФНтЮіЪНЮЊy= -![]() x2+
x2+![]() x+2.
x+2.
ЃЈ2ЃЉ
НтЃКШчЭМЃЌЙ§ЕуDзїDGЁЭxжсгкЕуGЃЌЙ§ЕуEзїEHЁЭxжсгкЕуH.
вРЬтПЩЕУЃК![]()
НтЕУ![]()
ЁрХзЮяЯпL1ЕФНтЮіЪНЮЊy=-x2+ЃЈm-4ЃЉx+4m.
ЁрЕуDЕФзјБъЮЊЃЈ-![]() ,
,![]() ЃЉ.
ЃЉ.
ЁрDG=![]() =
=![]() ,AG=
,AG=![]() .
.
ЭЌРэПЩЕУЃЌХзЮяЯпL2ЕФНтЮіЪНЮЊy=-x2+ЃЈm+4ЃЉx-4m
EH=![]() =
=![]() ЃЌBH=
ЃЌBH=![]() .
.
ЁпAFЁЭBFЃЌDGЁЭxжсЃЌEHЁЭxжс
ЁрЁЯAFB=ЁЯAGD=ЁЯEHB=90Ёу
ЁрЁЯADG=ЁЯABF=90Ёу-ЁЯBAF
ЁрЁїADGЁзЁїEBH
Ёр![]() =
=![]() .
.
Ёр =
=![]()
Ёрm=2![]() Лђm=-2
Лђm=-2![]() .
.

ЃЈ3ЃЉ
НтЃКДцдкЃЌР§Шчa=-![]() ,a=-
,a=-![]() .
.
ЁОНтЮіЁПЃЈ1ЃЉАбaЁЂmДњШыЕУЕНвбжЊЕуЃЌАбЕуДњШыКЏЪ§НтЮіЪНЙЙГЩЗНГЬзщЃЌИљОнД§ЖЈЯЕЪ§ЗЈПЩЧѓГіКЏЪ§НтЮіЪН.
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуDзїDGЁЭxжсгкЕуGЃЌЙ§ЕуEзїEHЁЭxжсгкЕуHЃЌАбa=-1ДњШыКЏЪ§НтЮіЪНЃЌШЛКѓНсКЯЃЈm,0ЃЉКЭЃЈ-4ЃЌ0ЃЉДњШыПЩНтГіКЏЪ§НтЮіЪНL1 ЃЌ ШЛКѓЗжБ№ЧѓГіDЕузјБъЃЌЕУЕНDG,AGЕФГЄЃЌЭЌРэЕУЕНL2;ЧѓЕУEH,BHЕФГЄЃЌдйИљОнШ§НЧаЮЯрЫЦЕФХаЖЈгыаджЪЙЙдьЗНГЬЧѓНтМДПЩ.
ЃЈ3ЃЉИљОнЧАУцЕФНтД№ЃЌжБНгаДГіМДПЩ.
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеЯрЫЦШ§НЧаЮЕФвЛЧаЖдгІЯпЖЮ(ЖдгІИпЁЂЖдгІжаЯпЁЂЖдгІНЧЦНЗжЯпЁЂЭтНгдВАыОЖЁЂФкЧадВАыОЖЕШЃЉЕФБШЕШгкЯрЫЦБШЃЛЯрЫЦШ§НЧаЮжмГЄЕФБШЕШгкЯрЫЦБШЃЛЯрЫЦШ§НЧаЮУцЛ§ЕФБШЕШгкЯрЫЦБШЕФЦНЗНВХФме§ШЗНтД№ДЫЬтЃЎ