Question

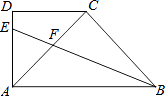
【题目】如图（1）是一个六角星的纸板，其中六个锐角都为60°，六个钝角都为120°，每条边都相等，现将该纸板按图（2）切割，并无缝隙无重叠地拼成矩形ABCD．若六角星纸板的面积为9 cm2 ， 则矩形ABCD的周长为（ ）
A.18cm
B.8 cm
C.（2 +6）cm
D.（6 +6）cm

Answer 1

【答案】D
【解析】解：如图，过点E作EF⊥AB于点F，
∵六个锐角都为60°，六个钝角都为120°，
∴设AE=xcm，则AD=3x，
∵∠AEB=120°，
∴∠EAB=30°，
∴AB=2AF=2xcos30°，
∵六角星纸板的面积为9 cm2 ，
∴ABAD=9 ，即2xcos30°3x=9 ，解得x= ，
∴AD=3 ，AB=3，
∴矩形ABCD的周长=2（3 +3）=（6 +6）cm．
故选D．
【考点精析】掌握矩形的性质是解答本题的根本，需要知道矩形的四个角都是直角，矩形的对角线相等．