题目内容
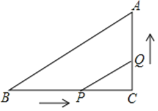
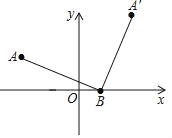
【题目】已知,如图,抛物线y=﹣x2+bx+c与x轴,y轴分别相交于点A(﹣1,0),B(0,3)两点,其顶点为D,

(1)求该抛物线的解析式;
(2)若抛物线与x轴另一个交点为E,求四边形ABDE的面积.
【答案】(1)该抛物线的解析式为:y=﹣x2+2x+3;
(2)S四边形ABDE=9.
【解析】
(1)根据待定系数法求解即可;
(2)根据坐标系中求图形面积的方法将所求四边形转化为两个直角三角形和一个直角梯形的面积的和即可.
解:(1)将点A(﹣1,0),B(0,3)两点代入解析式可得:
![]() ,解得:
,解得:![]() .
.
故该抛物线的解析式为:y=﹣x2+2x+3.
(2)由函数解析式为y=﹣x2+2x+3=![]() ,可得点D坐标为:(1,4),
,可得点D坐标为:(1,4),
当y=0时,﹣x2+2x+3=0,解得:x1=-1,x2=3,∴点E坐标为(3,0),
过点D作DF⊥x轴,交x轴于点F,

则点F坐标为(1,0),
从而可得S△ABO=![]() ,
,
S梯形BOFD=![]() (BO+DF)×OF=
(BO+DF)×OF=![]() ,S△DFE=
,S△DFE=![]() EF×DF=4,
EF×DF=4,
故可得S四边形ABDE=S△ABO+S梯形BOFD+S△DFE=9.

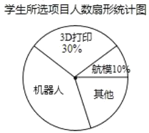
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m= ,n= ;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 °;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
【题目】甲、乙两组同时加工某种零件,甲组每小时加工80件,乙组加工的零件数量y(件)与时间x(小时)为一次函数关系,部分数据如下表所示.
x(小时) | 2 | 4 | 6 |
y(件) | 50 | 150 | 250 |
(1)求y与x之间的函数关系式;
(2)甲、乙两组同时生产,加工的零件合在一起装箱,每满340件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?