题目内容
23、如图(1),将两块直角三角板的直角顶点C叠放在一起,
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=40°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)

(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=40°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)

分析:(1)根据余角的定义求得,
(2)由于是两直角三角形板重叠,重叠的部分就比90°+90°减少的部分,所以若∠DCE=35°,则∠ACB的度数为180°-40°=140°,
(3)由于∠ACD=∠ECB=90°,重叠的度数就是∠ECD的度数,所以∠ACB+∠DCE=180°,
(4)根据重叠的部分实质是两个角的重叠可得.
(2)由于是两直角三角形板重叠,重叠的部分就比90°+90°减少的部分,所以若∠DCE=35°,则∠ACB的度数为180°-40°=140°,
(3)由于∠ACD=∠ECB=90°,重叠的度数就是∠ECD的度数,所以∠ACB+∠DCE=180°,
(4)根据重叠的部分实质是两个角的重叠可得.
解答: 解:(1)∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
解:(1)∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
∴∠ACE=∠BCD(同角的余角相等),
(2)∵∠DCE=40°,
∴∠ACE=50°,
∴∠ACB=∠ACE+∠BCE=50°+90°=140°,
(3)∠ACB+∠DCE=180°,
∵∠ACB=∠ACD+∠BCD,
∴∠ACB+∠DCE=∠ACD+∠BCD+∠DCE,
=∠ACD+∠BCE=180°,
(4)成立.
 解:(1)∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
解:(1)∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,∴∠ACE=∠BCD(同角的余角相等),
(2)∵∠DCE=40°,
∴∠ACE=50°,
∴∠ACB=∠ACE+∠BCE=50°+90°=140°,
(3)∠ACB+∠DCE=180°,
∵∠ACB=∠ACD+∠BCD,
∴∠ACB+∠DCE=∠ACD+∠BCD+∠DCE,
=∠ACD+∠BCE=180°,
(4)成立.
点评:本题主要考查了余角的定义以及重叠的部分实质是两个角的重叠,难度适中.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
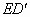 与AB相交于点F,请证明:
与AB相交于点F,请证明: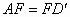 .
.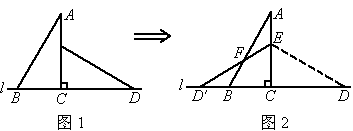


 如图,有一块长32m,宽24m的长方形草坪,其中有两条直道将草坪分为四块,则分成四块草坪的总面积是________.
如图,有一块长32m,宽24m的长方形草坪,其中有两条直道将草坪分为四块,则分成四块草坪的总面积是________.