Question

【题目】如图，正比例函数y=2x的图象与反比例函数y= 的图象交于A、B两点，过点A作AC垂直x轴于点C，连结BC．若△ABC的面积为2．
（1）求k的值；
（2）x轴上是否存在一点D，使△ABD为直角三角形？若存在，求出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵反比例函数与正比例函数的图象相交于A、B两点，

∴A、B两点关于原点对称，

∴OA=OB，

∴△BOC的面积=△AOC的面积=2÷2=1，

又∵A是反比例函数y= 图象上的点，且AC⊥x轴于点C，

∴△AOC的面积= |k|，

∴ |k|=1，

∵k＞0，

∴k=2．

故这个反比例函数的解析式为y= ；

（2）x轴上存在一点D，使△ABD为直角三角形．

将y=2x与y= 联立成方程组得：

，

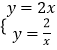解得： ， ，

∴A（1，2），B（﹣1，﹣2），

①当AD⊥AB时，如图1，

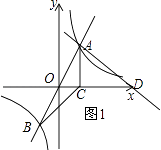
设直线AD的关系式为y=﹣ x+b，

将A（1，2）代入上式得：b= ，

∴直线AD的关系式为y=﹣ x+ ，

令y=0得：x=5，

∴D（5，0）；

②当BD⊥AB时，如图2，

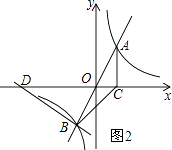
设直线BD的关系式为y=﹣ x+b，

将B（﹣1，﹣2）代入上式得：b=﹣ ，

∴直线AD的关系式为y=﹣ x﹣ ，

令y=0得：x=﹣5，

∴D（﹣5，0）；

③当AD⊥BD时，如图3，

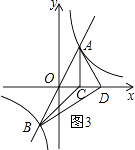
∵O为线段AB的中点，

∴OD= AB=OA，

∵A（1，2），

∴OC=1，AC=2，

由勾股定理得：OA= = ，

∴OD= ，

∴D（ ，0）．

根据对称性，当D为直角顶点，且D在x轴负半轴时，D（﹣ ，0）．

故x轴上存在一点D，使△ABD为直角三角形，点D的坐标为（5，0）或（﹣5，0）或（ ，0）或（﹣ ，0）．

【解析】（1）首先根据反比例函数与正比例函数的图象特征，可知A、B两点关于原点对称，则O为线段AB的中点，故△BOC的面积等于△AOC的面积，都等于1，然后由反比例函数y= 的比例系数k的几何意义，可知△AOC的面积等于 |k|，从而求出k的值；（2）先将y=2x与y= 联立成方程组，求出A、B两点的坐标，然后分三种情况讨论：①当AD⊥AB时，求出直线AD的关系式，令y=0，即可确定D点的坐标；②当BD⊥AB时，求出直线BD的关系式，令y=0，即可确定D点的坐标；③当AD⊥BD时，由O为线段AB的中点，可得OD= AB=OA，然后利用勾股定理求出OA的值，即可求出D点的坐标．