题目内容
如图,两个反比例函数 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )

 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
| A.3 | B.4 | C. | D.5 |
C
试题分析:设P的坐标是(a,
 ),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可.
),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可.解:∵点P在y=
 上,
上,∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a,
 )(a为正数),
)(a为正数),∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=﹣
 上,
上,∴A的坐标是(a,﹣
 ),
),∵PB⊥y轴,
∴B的纵坐标是
 ,
,∵B在y=﹣
 上,
上,∴代入得:
 =﹣
=﹣ ,
,解得:x=﹣2a,
∴B的坐标是(﹣2a,
 ),
),∴PA=|
 ﹣(﹣
﹣(﹣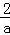 )|=
)|= ,PB=|a﹣(﹣2a)|=3a,
,PB=|a﹣(﹣2a)|=3a,∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是:
 PA×PB=
PA×PB= ×
× ×3a=
×3a= .
.故选C.
点评:本题考查了反比例函数和三角形面积公式的应用,关键是能根据P点的坐标得出A、B的坐标,本题具有一定的代表性,是一道比较好的题目.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 (度)与镜片焦距
(度)与镜片焦距 (米)成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数
(米)成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数 (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+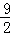 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.
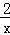 的图象如图所示,在同一直角坐标系内,如果将直线y=﹣x+1沿y轴向上平移2个单位后,那么所得直线与函数y=
的图象如图所示,在同一直角坐标系内,如果将直线y=﹣x+1沿y轴向上平移2个单位后,那么所得直线与函数y= 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )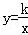 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)
 交矩形OABC的边分别于点D、E,若BD=2AD,且四边形ODBE的面积为8,则k= ______ .
交矩形OABC的边分别于点D、E,若BD=2AD,且四边形ODBE的面积为8,则k= ______ .
 上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为 ( )
上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为 ( )