Question

东方山是鄂东南地区的佛教胜地，月亮山是黄荆山脉第二高峰，山顶上有黄石电视塔．据黄石地理资料记载：东方山海拔453.20米，月亮山海拔442.00米，一飞机从东方山到月亮山方向水平飞行，在东方山山顶D的正上方A处测得月亮山山顶C的俯角为α，在月亮山山顶C的正上方B处测得东方山山顶D处的俯角为β，如图．已知tanα=0.1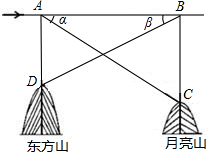5987，tanβ=0.15847，若飞机的飞行速度为180米/秒，则该飞机从A到B处需多少时间？（精确到0.1秒）

Answer 1

分析：根据tanα=

11.2+BM

AB

，tanβ=

AD

AB

，求出AB=8000米，进而求出该飞机从A到B 处需要时间．

解答：解：过D点作DM⊥BC，垂足为M，则BM=AD，
∵东方山海拔453.20米，月亮山海拔442.00米，
∴CM=BC-AD=453.20-442.00=11.2（米），
tanα=

11.2+BM

AB

，则AB=

11.2+BM

tanα

，
tanβ=

AD

AB

，则AB=

AD

tanβ

，
∴

11.2+BM

tanα

=

AD

tanβ

，
∵tanα=0.15987，tanβ=0.15847，AD=BM，
AD=11.2×1584.7÷14=1267.76（米），
AB=

1267.76

0.15847

=8000米，
∴该飞机从A到B处需8000÷180≈44.4s，
答：该飞机从A到B处需44.4s．

点评：此题主要考查了解直角三角形的应用，根据已知得出tanα=

11.2+BM

AB

，tanβ=

AD

AB

是解决问题的关键．