题目内容
如图，两个边长都为1的正方形，其中一个正方形的顶点在另一个正方形的对角线交点上，并且绕该交点旋转，求两个正方形重叠部分（阴影）的面积．
【答案】
【解析】
试题分析：根据正方形的性质可以推出△OKA≌△ODH，即可得到重叠部分的面积为△OAD的面积.
∵四边形ABDC与OEFM都是正方形，
∴∠OAK=∠ODH=45°，OA=OD，∠AOK=∠DOH=90°-∠AOH，
∴△OKA≌△ODH，
∴四边形OKAH的面积=△OKA的面积+△AOH的面积= △ODH的面积+△AOH的面积=△OAD的面积，
∴两个正方形重叠部分的面积
考点：本题考查的是正方形的性质，全等三角形的判定和性质
点评：解答本题的关键是熟练掌握正方形的四条边相等，四个角都是直角，对角线相等且互相垂直平分，对角线平分对角.
练习册系列答案
相关题目
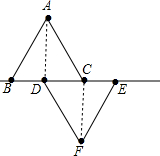上，连接AD及CF．
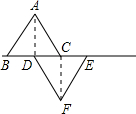上，连接AD、CF．若BD=3cm，△ABC沿着BE的方向以每秒1cm的速度运动，设△ABC运动时间为t秒，
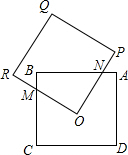如图所示，两个边长都为2的正方形ABCD和OPQR，如果O点正好是正方形ABCD的中心，而正方形OPQR可以绕O点旋转，那么它们重叠部分的面积为（ ）
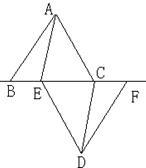21、如图，已知△ABC和△DEF是两个边长都为8cm的等边三角形，且点B，E，C，F在同一直线上，连接AE，DC．