Question

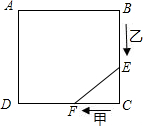如图；已知甲、乙分别从正方形ABCD广场的顶点B、C两点同时出发，甲由C 向D运动，乙由B向C运动，甲的速度是1千米/分，乙的速度是2千米/分．若正方形广场的周长为40千米，问：几分钟后甲、乙两之间相距2

10

千米？（友情提示：可以用直角三角形的勾股定理求解）

Answer 1

分析：本题可设时间为x分钟，依题意得CF=x，则BE=2x，周长为40km，边长为10km，CE=10-2x，利用勾股定理列方程求解．

解答：解：设x分钟后两车相距2

10

km，
此时甲运动到F点，乙运动到E点，
可知：FC=x，EC=10-2x，
在Rt△ECF中，x²+（10-2x）²=（2

10

）²，
解得：x₁=2，x₂=6，
当x=2时，FC=2，EC=10-4=6＜10符合题意，
当x=6时，FC=6，EC=10-12=-2＜0不符合题意，舍去，
答：2分钟后，两车相距2

10

千米．

点评：此题考查了勾股定理的应用，根据路程=速度×时间，表示线段的长度，将问题转化到三角形中，利用勾股定理或者面积关系建立等量关系，是解应用题常用的方法．