题目内容
如图,已知E是平行四边形ABCD的边AB上的点,连接DE.
(1)在∠ABC的内部,作射线BM交线段CD于点F,使∠CBF=∠ADE;
(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)在(1)的条件下,求证:△ADE≌△CBF.

考点:
作图—复杂作图;全等三角形的判定;平行四边形的性质。
分析:
(1)作∠CBM=∠ADE,其中BM交CD于F;
(2)根据平行四边形的性质可得∠A=∠C,AD=BC,由ASA可证△ADE≌△CBF.
解答:
(1)解:作图基本正确即可评3分.
(2)证明:∵四边形ABCD是平行四边形
∴∠A=∠C,AD=BC…5分
∵∠ADE=∠CBF…6分
∴△ADE≌△CBF(ASA).

点评:
综合考查了角的作图,平行四边形的性质和全等三角形的判定的知识,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论: 如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点.
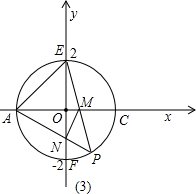
如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点. 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是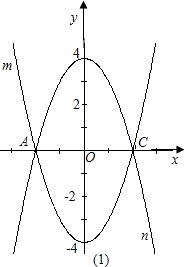

 如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为
如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为