题目内容
将1,2,3,4,5这五个数字排成一排,最后一个数是奇数,且使得其中任意连续三个数之和都能被这三个数中的第一个数整除,那么满足要求的排法有( )
| A.2种 | B.3种 | C.4种 | D.5种 |
法一:设a1,a2,a3,a4,a5是1,2,3,4,5的一个满足要求的排列.
首先,对于a1,a2,a3,a4,不能有连续的两个都是偶数,否则,这两个之后都是偶数,与已知条件矛盾.
又如果ai(1≤i≤3)是偶数,ai+1是奇数,则ai+2是奇数,这说明一个偶数后面一定要接两个或两个以上的奇数,除非接的这个奇数是最后一个数.
所以a1,a2,a3,a4,a5只能是:偶,奇,奇,偶,奇,有如下5种情形满足条件:
2,1,3,4,5;
2,3,5,4,1;
2,5,1,4,3;
4,3,1,2,5;
4,5,3,2,1.
法二:第一位是2,后面两位奇数任意:21345、23145、21543、25143、23541、25341
第一位是4,后面两位奇数不能是1、5或5、1:41325、43125、43521、45321
排除:23145、21543、25341、41325、43521
还剩:21345、25143、23541、43125、45321
所以共有5种排法
故选:D.
首先,对于a1,a2,a3,a4,不能有连续的两个都是偶数,否则,这两个之后都是偶数,与已知条件矛盾.
又如果ai(1≤i≤3)是偶数,ai+1是奇数,则ai+2是奇数,这说明一个偶数后面一定要接两个或两个以上的奇数,除非接的这个奇数是最后一个数.
所以a1,a2,a3,a4,a5只能是:偶,奇,奇,偶,奇,有如下5种情形满足条件:
2,1,3,4,5;
2,3,5,4,1;
2,5,1,4,3;
4,3,1,2,5;
4,5,3,2,1.
法二:第一位是2,后面两位奇数任意:21345、23145、21543、25143、23541、25341
第一位是4,后面两位奇数不能是1、5或5、1:41325、43125、43521、45321
排除:23145、21543、25341、41325、43521
还剩:21345、25143、23541、43125、45321
所以共有5种排法
故选:D.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:
将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:| 操作次数 | 1 | 2 | 3 | 4 | … |
| 所得正方形的总个数 | 4 | 7 | 10 | 13 | … |
(2)从表格和第(1)题的结果中你发现了什么?我发现
(3)请你根据你的发现归纳出:当操作次数为n次时,得到的正方形的个数是
(4)仔细观察图形,请你利用图形揭示的规律进行下面的计算(要有揭示规律的过程):
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
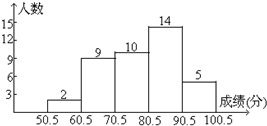 高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题: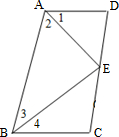 22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.
22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.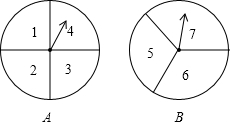 小亮获胜.
小亮获胜.