题目内容
(2010•襄阳)为了扶持农民发展农业生产,国家对购买农机的农户给予农机售价13%的政府补贴.某市农机公司筹集到资金130万元,用于一次性购进A,B两种型号的收割机30台.根据市场需求,这些收割机可以全部销售,全部销售后利润不少于15万元.其中,收割机的进价和售价见下表:| A型收割机 | B型收割机 | |
| 进价(万元/台) | 5.3 | 3.6 |
| 售价(万元/台) | 6 | 4 |
(1)试写出y与x的函数关系式;
(2)市农机公司有哪几种购进收割机的方案可供选择?
(3)选择哪种购进收割机的方案,农机公司获利最大?最大利润是多少?此种情况下,购买这30台收割机的所有农户获得的政府补贴总额W为多少万元?
【答案】分析:(1)y=(A型收割机售价-A型收割机进价)x+(B型收割机售价-B型收割机进价)×(30-x);
(2)购买收割机总台数为30台,用于购买收割机的总资金为130万元,总的销售后利润不少于15万元.可得到两个一元一次不等式.
(3)利用y与x的函数关系式y=0.3x+12来求最大利润.
解答:解:(1)y=(6-5.3)x+(4-3.6)(30-x)=0.3x+12(2分)
(2)依题意,有 (4分)
(4分)
即 ∴
∴ (5分)
(5分)
∵x为整数,∴x=10,11,12(6分)
即农机公司有三种购进收割机的方案可供选择:
方案1:购进A型收割机10台,购进B型收割机20台;
方案2:购A型收割机11台,购B型收割机19台;
方案3:购进A型收割机12台,购B型收割机18台.(7分)
(3)∵0.3>0,
∴一次函数y随x的增大而增大.(8分)
即当x=12时,y有最大值,y最大值=0.3×12+12=15.6(万元)(9分)
此时,W=6×13%×12+4×13%×18=18.72(万元).
答:选择第三种方案获利最大,最大利润为15.6万元,获得的政府补贴为18.72万元
点评:解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.
(2)购买收割机总台数为30台,用于购买收割机的总资金为130万元,总的销售后利润不少于15万元.可得到两个一元一次不等式.
(3)利用y与x的函数关系式y=0.3x+12来求最大利润.
解答:解:(1)y=(6-5.3)x+(4-3.6)(30-x)=0.3x+12(2分)
(2)依题意,有
 (4分)
(4分)即
 ∴
∴ (5分)
(5分)∵x为整数,∴x=10,11,12(6分)
即农机公司有三种购进收割机的方案可供选择:
方案1:购进A型收割机10台,购进B型收割机20台;
方案2:购A型收割机11台,购B型收割机19台;
方案3:购进A型收割机12台,购B型收割机18台.(7分)
(3)∵0.3>0,
∴一次函数y随x的增大而增大.(8分)
即当x=12时,y有最大值,y最大值=0.3×12+12=15.6(万元)(9分)
此时,W=6×13%×12+4×13%×18=18.72(万元).
答:选择第三种方案获利最大,最大利润为15.6万元,获得的政府补贴为18.72万元
点评:解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

练习册系列答案
相关题目
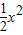 向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为 .
向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为 .
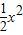 向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为 .
向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为 .
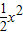 向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为 .
向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为 .