题目内容
如图所示,在边长为100米的正三角形路上,有甲、乙二人分别从两个不同的顶点处按逆时针方向同时出发,甲速度为4米/秒,乙速度为3米/秒.问出发多长时间,甲、乙二人第一次走在同一条边上?

答案:
解析:
提示:
解析:
|
解:分两种情况讨论: (1)若开始时甲在C处,乙在A处. 已知甲速>乙速,那么当甲走完AC边100米进入AB边时,乙还没有离开AB边. 而甲走100米需100÷4=25(秒). 即在这种情况下,出发25秒后,甲、乙二人第一次走在同一条边上. (2)若开始时甲在A处,乙在C处. 设甲经过x秒后追赶乙至正三角形的同一边上,则x需满足0≤200-(4x-3x)≤100, 即100≤x≤200. 当x=100时,乙的路程为3×100=300(米),说明乙又到了点C. 而此时甲的路程为4×100=400(米),说明甲到了点B,点B和C在同一边BC上,所以在这种情况下,出发100秒后,甲、乙二人第一次走在同一条边上. 答:略. 分析:由题意,知甲、乙有两种可能位置:(1)甲在乙后100米;(2)甲在乙后200米. |
提示:
|
本例第二种情况的连续不等式非常重要,忽略任何一边都不完整,所以对应用题一定要考虑周全. |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
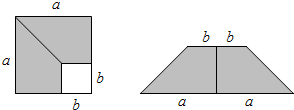

| A、(a-b)2=a2-2ab+b2 | B、(a+b)2=a2+2ab+b2 | C、a2-b2=(a+b)(a-b) | D、a2+ab=a(a+b) |

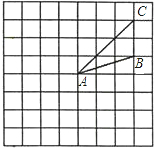 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离. 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.