题目内容
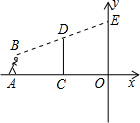如图，直角坐标平面内，小明站在点A（-10，0）处观察y轴，眼睛距地面1.5米，他的前方5米处有一堵墙DC，若墙高DC=2米，则小明在y轴上的盲区（即OE的长度）为分析：首先作出BM⊥EO，得出△BND∽△BME，即可得出
=
，再利用已知得出BN，BM，DN的长，即可求出EM，进而求出EO即可．
| BN |
| BM |
| DN |
| EM |
解答：
解：过点B作BM⊥EO，交CD于点N，
∵CD∥EO，
∴△BND∽△BME，
∴
=
，
∵点A（-10，0），
∴BM=10米，
∵眼睛距地面1.5米，
∴AB=CN=MO=1.5米，
∵DC=2米，
∴DN=2-1.5=0.5米，
∵他的前方5米处有一堵墙DC，
∴BN=5米，
∴
=
，
∴EM=1米，
∴EO=1+1.5=2.5米．
故答案为：2.5．
解：过点B作BM⊥EO，交CD于点N，∵CD∥EO，
∴△BND∽△BME，
∴
| BN |
| BM |
| DN |
| EM |
∵点A（-10，0），
∴BM=10米，
∵眼睛距地面1.5米，
∴AB=CN=MO=1.5米，
∵DC=2米，
∴DN=2-1.5=0.5米，
∵他的前方5米处有一堵墙DC，
∴BN=5米，
∴
| 5 |
| 10 |
| 0.5 |
| EM |
∴EM=1米，
∴EO=1+1.5=2.5米．
故答案为：2.5．
点评：此题主要考查的是相似三角形的应用以及盲区问题等知识，解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题，利用已知作出相似三角形进而得出EM的长．
练习册系列答案
相关题目
如图，在直角坐标平面内，已知点A的坐标（-5，0），
如图，直角坐标平面内，小明站在点A（-10，0）处观察y轴，眼睛距地面1.5米，他的前方5米处有一堵墙DC，若墙高DC=2米，则小明在y轴上的盲区（即OE的长度）为________米．
如图，直角坐标平面内，小明站在点A（-10，0）处观察y轴，眼睛距地面1.5米，他的前方5米处有一堵墙DC，若墙高DC=2米，则小明在y轴上的盲区（即OE的长度）为 米．