题目内容
(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2 ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
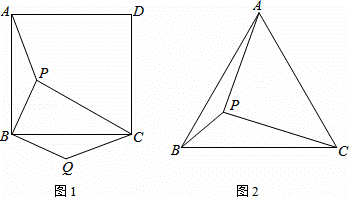
解:(1)连接PQ.
由旋转可知: ,QC=PA=3.
,QC=PA=3.

又∵ABCD是正方形,
∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,
即∠PBQ=90°,
∴∠PQB=45°,PQ=4.
则在△PQC中,PQ=4,QC=3,PC=5,
∴PC2=PQ2+QC2.
即∠PQC=90°.
故∠BQC=90°+45°=135°.
(2)将此时点P的对应点是点P′.

由旋转知,△APB≌△CP′B,即∠BPA=∠BP′C,P′B=PB=5,P′C=PA=12.
又∵△ABC是正三角形,
∴△ABP绕点B顺时针方向旋转60°,才使点A与C重合,
得∠PBP′=60°,
又∵P′B=PB=5,
∴△PBP′也是正三角形,即∠PP′B=60°,PP′=5.
因此,在△PP′C中,PC=13,PP′=5,P′C=12,
∴PC2=PP′2+P′C2.
即∠PP′C=90°.
故∠BPA=∠BP′C=60°+90°=150°.

练习册系列答案
相关题目
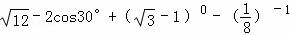 .
.
 B.2 C.﹣2 D. ﹣
B.2 C.﹣2 D. ﹣ )
) ﹣
﹣