题目内容
求证：等腰三角形底边上的任一点与两腰的距离之和等于一腰上的高。
解：已知：在△ABC中，AB=AC，DE⊥AB于EDF⊥AC于F，CG⊥AB于G。
求证：CG=DE + DF。
证明：过D作DH⊥CG交CG于点H
先证四边形EDHG为矩形
所以DE=GH
再证△CHD≌△DFC
所以DF=CH
所以CG=DE + DF
求证：CG=DE + DF。
证明：过D作DH⊥CG交CG于点H
先证四边形EDHG为矩形
所以DE=GH
再证△CHD≌△DFC
所以DF=CH
所以CG=DE + DF
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
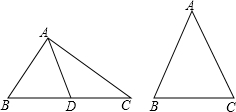下面两题任选一题
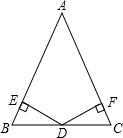求证：等腰三角形底边上的中点到两腰的距离相等．结合所给图形，把“已知”、“求证”补充完整，并完成证明过程．