Question

【题目】如图， 为⊙的直径，点在⊙上，连接、，过点的切线与的延长线交于点， ，交于点，交于点．

（）求证： ．

（）若⊙的半径为， ，求的长．

Answer 1

【答案】（）见解析　（）．

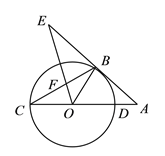
【解析】（1）连接OB．由切线的性质先证明∠OBE=∠EFB+∠CBO=90°，再由圆周角定理得出∠CBD=∠CBO+∠OBD=90°，故∠EBF=∠OBD，根据等腰三角形的性质可知∠OBD=∠CDB，故∠EBF=∠CDB，进而可得结论；

（2）由（1）可知∽∠OBE=90°，∠E=∠C，在Rt△BOE中，利用锐角三角函数的定义即可得出结论．

证明：（）∵，∴， （两直线平行，内错角相等，同位角相等）．

连接，

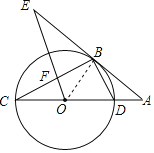
∵过点的切线与的延长线交于点，

∴OB⊥AE，

∴∠OBE=∠EFB+∠CBO=90°，

为⊙的直径，

∴∠CBD=∠CBO+∠OBD=90°，

∴∠EBF=∠OBD，

∵OB、OD是⊙O的半径，

∴OB=OD，

∴∠OBD=∠CDB，

∴∠EBF=∠CDB，

∵，

∴∠EFB=∠CBD，

∴∽．

（）由1）可知∽

∴∠OBE=90°，

∴∠E=∠C，

∵∠C=30°，

∴∠E=∠C=30°，

∵⊙O的半径为3，

在Rt△BOE中，∠OBE=90°，∠E =30°，OB=3，

∴，即，

∴的长为．