题目内容
如图,抛物线y=ax2-4ax+b交x轴于A(1,0)、B两点,交y轴于C(0,3);
(1)求抛物线的解析式;
(2)抛物线上是否存在点P,使∠PCB+∠ACB=45°?若存在,求出P点坐标;若不存在,请说明理由;
(3)将直线AC沿x轴的正方向平移,平移后的直线交y轴于点M,交抛物线于点N,问是否存在M、N使四边形ACMN为等腰梯形?若存在,求出M、N的坐标;若不存在,请说明理由.

解:(1)∵抛物线y=ax2-4ax+b交x轴于A(1,0)、B两点,交y轴于C(0,3);
∴将A(1,0),C(0,3),代入解析式即可求出:
0=a-4a+b,b=3,
∴a=1,
y=x2-4x+3;
(2)设P(m,n),
∵B点坐标为:(3,0),C点坐标为:(0,3),
∴CO=BO=3,
∴∠OCB=45°,
∵要使∠PCB+∠ACB=45°,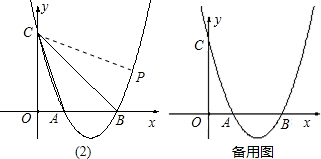
∴∠OCA=∠PCB,
∴cos∠OCA=cos∠PCB,
∵OA=1,OC=3,
∴cos∠OCA= ,
,
∴PC=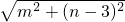 ,PB=
,PB=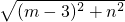 ,
,
BC=3 ,
,
cos∠PCB=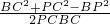 =
= ,
,
解得m= 或m=2,即n=
或m=2,即n= 或n=-1,
或n=-1,
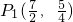 、P2(2,-1);
、P2(2,-1);
(3)作MN∥AC,CE⊥MN,AF⊥MN,QN⊥BO,
∴四边形CAFE是矩形,
∴∠CME=∠OCA,
∵∠OCA+∠CAO=90°,
∠MCE+∠OCA=90°,
∴∠MCE=∠CAO,
同理可得:要使四边形ACMN为等腰梯形,
∴∠CME=∠ANF,
∵AC∥MN,
∴直线MN的解析式可以设为:y=-3x+3+k,
联立y=x2-4x+3;
得出两图象在第四象限交点的横坐标为: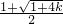 ,
,
分别代入两函数解析式即可得出:纵坐标为: +k-
+k-
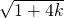 ,
,
∴AQ=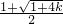 -1=
-1=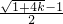 ,
,
QN= +k-
+k-
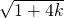 ,
,
∵MC=AN,
∴MC2=AQ2+QN2,
∴k2=(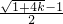 )2+(
)2+( +k-
+k-
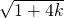 )2,
)2,
解得:k= ,
,
∴OM= +3=
+3= ,
,
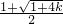 =
= ,
, +k-
+k-
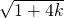 =-
=- ,
,
故此时: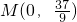 ;
;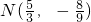 .
.
分析:(1)根据抛物线y=ax2-4ax+b交x轴于A(1,0),交y轴于C(0,3),直接求出即可;
(2)利用三角形对应角之间的关系得出;
(3)根据等腰梯形的性质得出∠CME=∠ANF,进而求出CM的长,以及M,N点的坐标.
点评:此题主要考查了待定系数法求二次函数解析式以及等腰梯形的性质,题目综合性较强,难度较大,需细心分析得出.
∴将A(1,0),C(0,3),代入解析式即可求出:
0=a-4a+b,b=3,
∴a=1,
y=x2-4x+3;
(2)设P(m,n),
∵B点坐标为:(3,0),C点坐标为:(0,3),
∴CO=BO=3,
∴∠OCB=45°,
∵要使∠PCB+∠ACB=45°,

∴∠OCA=∠PCB,
∴cos∠OCA=cos∠PCB,
∵OA=1,OC=3,
∴cos∠OCA=
 ,
,∴PC=
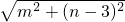 ,PB=
,PB=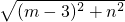 ,
,BC=3
 ,
,cos∠PCB=
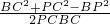 =
= ,
,解得m=
 或m=2,即n=
或m=2,即n= 或n=-1,
或n=-1,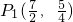 、P2(2,-1);
、P2(2,-1);(3)作MN∥AC,CE⊥MN,AF⊥MN,QN⊥BO,
∴四边形CAFE是矩形,
∴∠CME=∠OCA,
∵∠OCA+∠CAO=90°,
∠MCE+∠OCA=90°,
∴∠MCE=∠CAO,
同理可得:要使四边形ACMN为等腰梯形,
∴∠CME=∠ANF,
∵AC∥MN,

∴直线MN的解析式可以设为:y=-3x+3+k,
联立y=x2-4x+3;
得出两图象在第四象限交点的横坐标为:
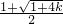 ,
,分别代入两函数解析式即可得出:纵坐标为:
 +k-
+k-
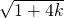 ,
,∴AQ=
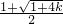 -1=
-1=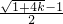 ,
,QN=
 +k-
+k-
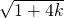 ,
,∵MC=AN,
∴MC2=AQ2+QN2,
∴k2=(
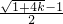 )2+(
)2+( +k-
+k-
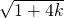 )2,
)2,解得:k=
 ,
,∴OM=
 +3=
+3= ,
,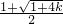 =
= ,
, +k-
+k-
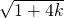 =-
=- ,
,故此时:
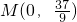 ;
;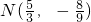 .
.分析:(1)根据抛物线y=ax2-4ax+b交x轴于A(1,0),交y轴于C(0,3),直接求出即可;
(2)利用三角形对应角之间的关系得出;
(3)根据等腰梯形的性质得出∠CME=∠ANF,进而求出CM的长,以及M,N点的坐标.
点评:此题主要考查了待定系数法求二次函数解析式以及等腰梯形的性质,题目综合性较强,难度较大,需细心分析得出.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).