题目内容
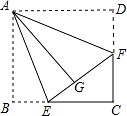
如图,正方形纸片 ABCD 的边长为 3,点 E、F 分别在边 BC、CD 上,将 AB、AD 分别和 AE、 AF 折叠,点 B、D 恰好都将在点 G 处,已知 BE=1,则 EF 的长为( )
A. 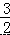 B.
B. 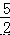 C.
C. 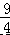 D.3
D.3
B【考点】翻折变换(折叠问题).
【专题】压轴题.
【分析】由正方形纸片 ABCD 的边长为 3,可得∠C=90°,BC=CD=3,由根据折叠的性质得:EG=BE=1, GF=DF,然后设 DF=x,在 Rt△EFC 中,由勾股定理 EF2=EC2+FC2,即可得方程,解方程即可求得 答案.
【解答】解:∵正方形纸片 ABCD 的边长为 3,
∴∠C=90°,BC=CD=3,
根据折叠的性质得:EG=BE=1,GF=DF, 设 DF=x,
则 EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2, 在 Rt△EFC 中,EF2=EC2+FC2,
即(x+1)2=22+(3﹣x)2, 解得:x= 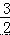 ,
,
∴DF= 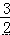 ,EF=1+
,EF=1+ 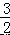 =
=  .
.
故选 B.
【点评】此题考查了折叠的性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合 思想与方程思想的应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
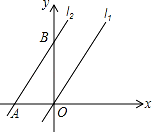
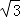 A.3 B.4 C.2
A.3 B.4 C.2 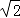 D.2
D.2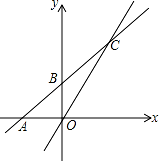
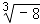 ﹣2
﹣2 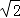 +(
+( 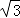 )2+|1﹣
)2+|1﹣ 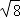 |
|
 SA D.SSS
SA D.SSS