题目内容
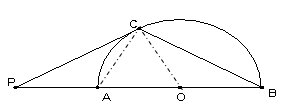
如图,点P在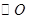 的直径BA的延长线上,AB=2PA,PC切
的直径BA的延长线上,AB=2PA,PC切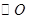 于点C,连结BC。
于点C,连结BC。
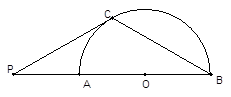
(1)求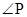 的正弦值;
的正弦值;
(2)若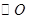 的半径r=2cm,求BC的长度。
的半径r=2cm,求BC的长度。
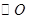 的直径BA的延长线上,AB=2PA,PC切
的直径BA的延长线上,AB=2PA,PC切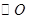 于点C,连结BC。
于点C,连结BC。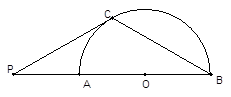
(1)求
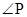 的正弦值;
的正弦值;(2)若
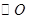 的半径r=2cm,求BC的长度。
的半径r=2cm,求BC的长度。解:(1)连结OC,
因为PC切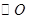 于点C,
于点C,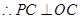
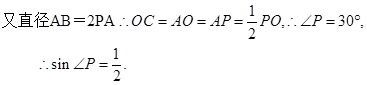
(或:在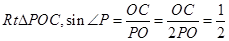 )
)
(2)连结AC,由AB是直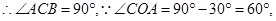
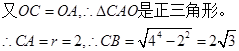

因为PC切
 于点C,
于点C,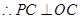
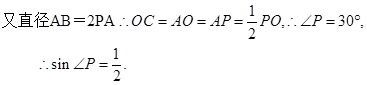
(或:在
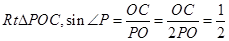 )
)(2)连结AC,由AB是直
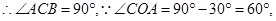
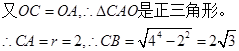
(1)连接OC,则PC⊥OC,又AB=2PA,则有OC=AO=AP=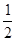 PO,于是∠P=30°,可证sin∠P=
PO,于是∠P=30°,可证sin∠P=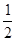 ;
;
(2)连接AC,证得△CAO是正三角形,那么CA=r=2,再根据勾股定理可求得CB的长
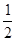 PO,于是∠P=30°,可证sin∠P=
PO,于是∠P=30°,可证sin∠P=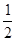 ;
;(2)连接AC,证得△CAO是正三角形,那么CA=r=2,再根据勾股定理可求得CB的长

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 1=
1=

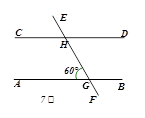
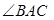 ,求作:线段MN, 使其同时满足下列3个条件(要求:用尺规作图,保留作图痕迹,不写作法和结论):
,求作:线段MN, 使其同时满足下列3个条件(要求:用尺规作图,保留作图痕迹,不写作法和结论):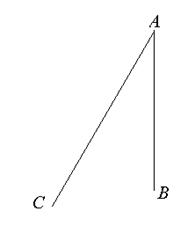

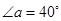 ,那么
,那么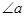 的补角等于 .
的补角等于 .