题目内容
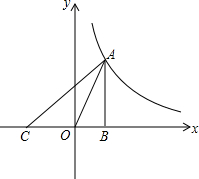 如图,Rt△ABC(∠ABC=90°)的顶点A是双曲线y=
如图,Rt△ABC(∠ABC=90°)的顶点A是双曲线y=| k | x |
(1)求出这两个函数的表达式和△ABC的面积;
(2)点M、N分别在x轴和y轴上,以A、C、M、N为顶点的四边形为平行四边形,求M、N的坐标.
分析:(1)根据S△ABO=1,求出k的值,从而得到一次函数与反比例函数的解析式,再根据一次函数解析式求出C点坐标,再将y=x+2和y=
组成方程组,求出A点坐标,然后根据三角形的面积公式求出△ABC的面积;
(2)分两种情况讨论,①AN∥MC,AN=MC时,四边形ANMC为平行四边形,再求出M、N的坐标;②MN∥AC,MN=AC时,四边形ACNM为平行四边形,再求出M、N的坐标.
| 2 |
| x |
(2)分两种情况讨论,①AN∥MC,AN=MC时,四边形ANMC为平行四边形,再求出M、N的坐标;②MN∥AC,MN=AC时,四边形ACNM为平行四边形,再求出M、N的坐标.
解答:解:(1)∵∠ABO=90°,S△ABO=1,
∴k=2S△ABO=2,
故一次函数解析式为y=x+2;反比例函数解析式为y=
;
当y=0时,对于x+2=0,x=-2;
C点坐标为(-2,0),
将y=x+2和y=
组成方程组得;
,
解得x=-1±
,y=1±
,
由于交点在第一象限,
故A点坐标为(-1+
,1+
).
∴S△ABC=
×BC×AB=
×(-1+
+2)×(1+
)=2+
;
(2)如图1,作AN⊥y轴,则AN∥MC,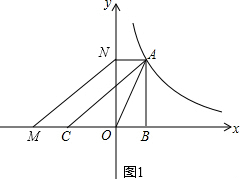
在OC上截取MC=AN,
故四边形ANMC为平行四边形.
∵AN=-1+
,
∴MC=-1+
,
有∵CO=2,
∴MO=2-1+
=1+
,
∵ON=AB=1+
,
∴N点坐标为(0,1+
),M点坐标为(1+
,0).
 如图2,当MN∥AC,MN=AC时,
如图2,当MN∥AC,MN=AC时,
四边形ACNM为平行四边形,
易得,△ABM≌△NOC,
∴AB=NO,
∴N点坐标为(0,1+
),
∵△ABC≌△NOM,
∴OM=BC=(-1+
+2)=1+
,
∴M点坐标为(1+
,0).
∴k=2S△ABO=2,
故一次函数解析式为y=x+2;反比例函数解析式为y=
| 2 |
| x |
当y=0时,对于x+2=0,x=-2;
C点坐标为(-2,0),
将y=x+2和y=
| 2 |
| x |
|
解得x=-1±
| 3 |
| 3 |
由于交点在第一象限,
故A点坐标为(-1+
| 3 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
(2)如图1,作AN⊥y轴,则AN∥MC,

在OC上截取MC=AN,
故四边形ANMC为平行四边形.
∵AN=-1+
| 3 |
∴MC=-1+
| 3 |
有∵CO=2,
∴MO=2-1+
| 3 |
| 3 |
∵ON=AB=1+
| 3 |
∴N点坐标为(0,1+
| 3 |
| 3 |
 如图2,当MN∥AC,MN=AC时,
如图2,当MN∥AC,MN=AC时,四边形ACNM为平行四边形,
易得,△ABM≌△NOC,
∴AB=NO,
∴N点坐标为(0,1+
| 3 |
∵△ABC≌△NOM,
∴OM=BC=(-1+
| 3 |
| 3 |
∴M点坐标为(1+
| 3 |
点评:本题考查了反比例函数综合题,涉及函数图象交点坐标与方程组的关系、平行四边形的判定与性质、三角形的面积公式、反比例函数系数k的几何意义等知识,旨在考查学生分析问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过
如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过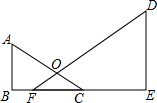 已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15.
已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15. (2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6
(2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6