题目内容
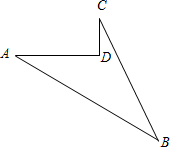 如图所示,由4条线段围成的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m.
如图所示,由4条线段围成的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m.(1)试说明:AC⊥BC;
(2)求这块地的面积.
分析:(1)连接AC,利用勾股定理求出AC的长度,再利用勾股定理的逆定理即可证明三角形ACB是直角三角形,进而证明AC⊥BC;
(2)由图形可知木板面积为这两三角形面积之差.
(2)由图形可知木板面积为这两三角形面积之差.
解答: (1)证明:连接AC,
(1)证明:连接AC,
∵在△ADC中,AD=4,DC=3,∠D=90°,
∴AC=5,
∵在△ACB中,AC=5,BC=12,AB=13,
∴BC2+AC2=122+52=169,AB2=132=169,
∴BC2+AC2=AB2,
∴△ABC为直角三角形,
∴AC⊥BC;
(2)由(1)可知三角形ABC和三角形ADC都是直角三角形,
∴木板的面积为:S△ACB-S△ADC=
×5×12-
×3×4=24.
 (1)证明:连接AC,
(1)证明:连接AC,∵在△ADC中,AD=4,DC=3,∠D=90°,
∴AC=5,
∵在△ACB中,AC=5,BC=12,AB=13,
∴BC2+AC2=122+52=169,AB2=132=169,
∴BC2+AC2=AB2,
∴△ABC为直角三角形,
∴AC⊥BC;
(2)由(1)可知三角形ABC和三角形ADC都是直角三角形,
∴木板的面积为:S△ACB-S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查正确运用勾股和勾股定理的逆定理的运用,善于观察题目的信息画图是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 12、如图所示,由A到B有①,②,③三条路线,最短的路线选①的理由是( )
12、如图所示,由A到B有①,②,③三条路线,最短的路线选①的理由是( )
 如图所示,由A到B有(1)(2)(3)三条路线,最短的路线选(1)的理由是( )
如图所示,由A到B有(1)(2)(3)三条路线,最短的路线选(1)的理由是( )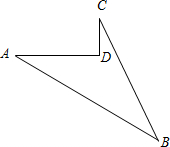 如图所示,由4条线段围成的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m.
如图所示,由4条线段围成的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m.