题目内容
 如图,已知点P、C是函数y=
如图,已知点P、C是函数y=| 1 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、S1与S2的大小不能确定 |
分析:过C点作CD⊥x轴于D,过P点作PG⊥y轴于G,根据反比例函数y=
中k的几何意义,及组合图形相互间的面积关系可知S1与S2的关系.
| k |
| x |
解答: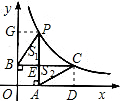 解:过C点作CD⊥x轴于D,过P点作PG⊥y轴于G,
解:过C点作CD⊥x轴于D,过P点作PG⊥y轴于G,
依据比例系数k的几何意义可得
S长方形BCDO=S长方形APGO,
∵S1=
(S矩形APGO-S矩形AEBO),
S2=
(S矩形BCDO-S矩形AEBO),
∴S1=S2.
故选B.
 解:过C点作CD⊥x轴于D,过P点作PG⊥y轴于G,
解:过C点作CD⊥x轴于D,过P点作PG⊥y轴于G,依据比例系数k的几何意义可得
S长方形BCDO=S长方形APGO,
∵S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
∴S1=S2.
故选B.
点评:本题考查反比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|.该知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
相关题目
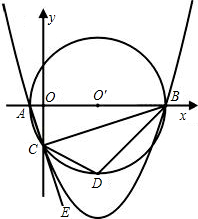 什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标. 如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线. (2012•黑龙江)如图,已知点E、F是平行四边形ABCD对角线上的两点,请添加一个条件
(2012•黑龙江)如图,已知点E、F是平行四边形ABCD对角线上的两点,请添加一个条件 如图,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm,求线段AB的长.
如图,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm,求线段AB的长.