题目内容
(1)如果a、b、c是非零有理数,那么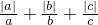 的所有可能值是______.
的所有可能值是______.
(2)从1,2,3…10,每个数前面任意添上正负号,则得到这十个新数和的绝对值的最小值为______.
(3)22011+32012的个位数字是______.
解:①当a>0,b>0,c>0时,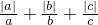 =
=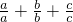 =1+1+1=3;
=1+1+1=3;
②当a<0,b<0,c<0时,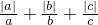 =
= =-1-1-1=-3;
=-1-1-1=-3;
③当a>0,b>0,c<0时,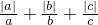 =
= =1+1-1=1;
=1+1-1=1;
同理,a>0,b<0,c>0;a<0,b>0,c>0时原式的值均为1.
④当a<0,b<0,c>0时,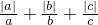 =
=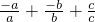 =-1-1+1=-1;
=-1-1+1=-1;
同理,当a<0,b>0,c<0;a>0,b<0,c<0时原式的值均为-1.
故答案为:3,1,-1,-3;
(2)∵1+2+3+…+10=55,
∴从1,2,3…10,每个数前面任意添上正负号,得到这十个新数和的绝对值的最小值为:28与27的差,
∴这十个新数和的绝对值的最小值为:1.
故答案为:1;
(3)解:∵3n的个位数字是3,9,7,1四个一循环,2012÷4=503,
∴32012个位数字和34的个位数字是相同的,即为1.
21=2,22=4,23=8,24=16,25=32,26=64,…,
2011÷4=502余3,
∴22011的个位数字是8.
∴22011+32012的个位数字是:8+1=9.
故答案为:9.
分析:(1)根据绝对值的性质,将绝对值符号去掉,然后计算.由于不知道a、b、c的符号,故需分类讨论.
(2)根据1+2+3+…+10=55,即可得出得到这十个新数和的绝对值的最小值是1的绝对值,即可得出答案;
(3)根据31=3,32=9,33=27,34=81,可知3n的个位数字是3,9,7,1四个一循环,求出21=2,22=4,23=8,24=16,25=32,26=64,得出规律2,4,8,6;根据规律求出即可.
点评:此题考查了数字的规律问题以及绝对值规律的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0,解答时要注意分类讨论.能够从特殊推广到一般,正确发现数字规律是解题关键.
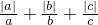 =
=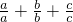 =1+1+1=3;
=1+1+1=3;②当a<0,b<0,c<0时,
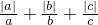 =
= =-1-1-1=-3;
=-1-1-1=-3;③当a>0,b>0,c<0时,
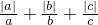 =
= =1+1-1=1;
=1+1-1=1;同理,a>0,b<0,c>0;a<0,b>0,c>0时原式的值均为1.
④当a<0,b<0,c>0时,
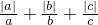 =
=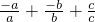 =-1-1+1=-1;
=-1-1+1=-1;同理,当a<0,b>0,c<0;a>0,b<0,c<0时原式的值均为-1.
故答案为:3,1,-1,-3;
(2)∵1+2+3+…+10=55,
∴从1,2,3…10,每个数前面任意添上正负号,得到这十个新数和的绝对值的最小值为:28与27的差,
∴这十个新数和的绝对值的最小值为:1.
故答案为:1;
(3)解:∵3n的个位数字是3,9,7,1四个一循环,2012÷4=503,
∴32012个位数字和34的个位数字是相同的,即为1.
21=2,22=4,23=8,24=16,25=32,26=64,…,
2011÷4=502余3,
∴22011的个位数字是8.
∴22011+32012的个位数字是:8+1=9.
故答案为:9.
分析:(1)根据绝对值的性质,将绝对值符号去掉,然后计算.由于不知道a、b、c的符号,故需分类讨论.
(2)根据1+2+3+…+10=55,即可得出得到这十个新数和的绝对值的最小值是1的绝对值,即可得出答案;
(3)根据31=3,32=9,33=27,34=81,可知3n的个位数字是3,9,7,1四个一循环,求出21=2,22=4,23=8,24=16,25=32,26=64,得出规律2,4,8,6;根据规律求出即可.
点评:此题考查了数字的规律问题以及绝对值规律的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0,解答时要注意分类讨论.能够从特殊推广到一般,正确发现数字规律是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果关于x的不等式组
无解,则m的取值范围是( )
|
| A、m>3 | B、m≥3 |
| C、m<3 | D、m≤3 |
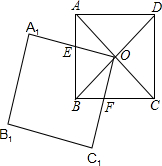 于点E,OC1交BC于点F.
于点E,OC1交BC于点F. ,请问小军至少几次进入迷宫中心?
,请问小军至少几次进入迷宫中心?