Question

【题目】如图，△POA1、△P2A1A都是等腰直角三角形，直角顶点P、P2在函数y= （x＞0）的图象上，斜边OA1、A1A都在x轴上，则点A的坐标是（ ）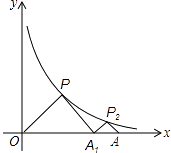

A.（4，0）
B.（4 ，0）
C.（2，0）
D.（2 ，0）

Answer 1

【答案】B
【解析】解：过P作PB⊥x轴于B，如图

∵△POA是等腰直角三角形，
∴BP=BO=BA，
设OB=a，则P点坐标为（a，a），
∵点P在函数y= （x＞0）的图象上，
∴a2=4，
∴a=2，
∴OA=2a=4，
∴A点坐标为（4，0）．
设P2（4+b，b），则b（4+b）=4，解得b1=﹣2﹣2 （舍去），b2=﹣2+2 ，
∴AA1=2b=﹣4+4 ，
∴OA=4﹣4+4 =4 ，
∴A（4 ，0）．
故选B．