��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���������ABCD�����ڲ���ÿ����������²�������ÿ����ĺᡢ�����궼����ͬһ��ʵ��a�����õ��ĵ�������ƽ��m����λ��������ƽ��n����λ��m��0��n��0�����õ�������A'B'C'D'�����ڲ��ĵ㣬���е�A��B�Ķ�Ӧ��ֱ�ΪA'��B'����֪������ABCD�ڲ���һ����F��������������õ��Ķ�Ӧ��F'���F�غϣ����F�������ǣ�������
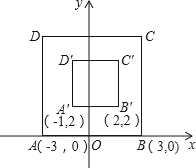
A. ��1��4�� B. ��1��5�� C. ����1��4�� D. ��4��1��
���𰸡�A
��������
���ȸ��ݵ�A��A�䣬B��B���ĵ������ɵ÷�����![]()
![]() ����ɵ�a��m��n��ֵ����F�������Ϊ��x��y������F����F�غϿ��г������飬�ٽ�ɵ�F�����꣮
����ɵ�a��m��n��ֵ����F�������Ϊ��x��y������F����F�غϿ��г������飬�ٽ�ɵ�F�����꣮
�ɵ�A��A�����ɵ÷�����
![]()
��B��B��,�ɵ÷�����![]() ��
��
���
��F�������Ϊ(x,y),��F����F�غϵõ�������
���![]() ��
��
��F(1,4).
��ѡA.

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ