题目内容
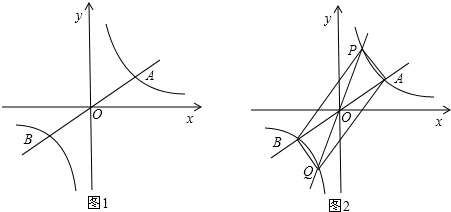
如图1,已知直线y1=kx+4与函数 的图象相交于点A(1,3)、B( m,1)两点.
的图象相交于点A(1,3)、B( m,1)两点.
(1)求a、k、m的值;
(2)求y1>y2时x的取值范围(请直接写出答案);
(3)求△AOB的面积;
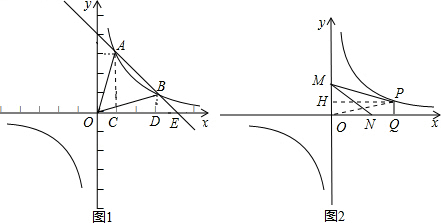
(4)如图2,M(0,2)、N(2,0),在上述函数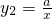 (x>0)的图象上取一点P(点P的横坐标大于2),过点P作PQ⊥x轴,垂足是Q.若四边形MNQP的面积等于2,求P点的坐标.
(x>0)的图象上取一点P(点P的横坐标大于2),过点P作PQ⊥x轴,垂足是Q.若四边形MNQP的面积等于2,求P点的坐标.
解:(1)将点A(1,3)代入y1=kx+4,可得k+4=3,
解得:k=-1;
将点A(1,3)代入,y2= ,可得3=
,可得3=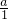 ,
,
解得:a=3,即可得y2= ,
,
将点B(m,1)代入y2= ,可得1=
,可得1= ,
,
解得:m=3;
综上可得:k=-1,a=3,m=3;
(2)结合函数图象可得:当x<0或1<x<3时,y1>y2.
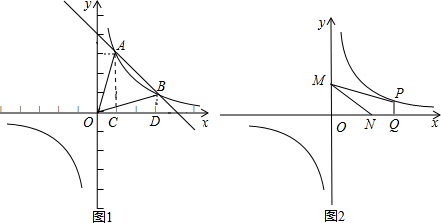
(3)
由y1=-x+4可得点E的坐标为(4,0),
则S△AOE= OE×A纵=6,S△BOE=
OE×A纵=6,S△BOE= OE×B纵=2,
OE×B纵=2,
故可得S△AOB=S△AOE-S△BOE=4;
(4)设点P的坐标为(x, ),
),
S△MPO= OM×P横=x,S△POQ=
OM×P横=x,S△POQ= |a|=
|a|= ,S△MON=
,S△MON= OM×ON=2,
OM×ON=2,
则S△MOP+S△OPQ=S△MON+S四边形MNQP=S四边形MPQO,
即x+ =2+2,
=2+2,
解得:x= ,则
,则 =
= ,
,
故点P的坐标为:(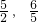 ).
).
分析:(1)将点A(1,3),代入y1、y2可得出k、a的值,然后将点B(m,1)代入y2可得出m的值.
(2)根据图象即可得出y1>y2时x的取值范围.
(3)求出直线AB与x轴的交点E的坐标,然后求出S△AOE、S△BOE,根据S△AOB=S△AOE-S△BOE,可得出△AOB的面积.
(4)根据(1)中求得a的值,可设点P(x, ),连接OP,根据S△MOP+S△OPQ=S△MON+S四边形MNQP,可得出x的值,继而得出点P的坐标.
),连接OP,根据S△MOP+S△OPQ=S△MON+S四边形MNQP,可得出x的值,继而得出点P的坐标.
点评:本题考查了反比例函数综合题,涉及了待定系数法求函数解析式、不规则图形面积的求法及反比例函数k的几何意义,综合性较强,解答本题要求我们熟悉各个知识点,能将所学的知识融会贯通,难度较大.
解得:k=-1;
将点A(1,3)代入,y2=
 ,可得3=
,可得3=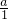 ,
,解得:a=3,即可得y2=
 ,
,将点B(m,1)代入y2=
 ,可得1=
,可得1= ,
,解得:m=3;
综上可得:k=-1,a=3,m=3;
(2)结合函数图象可得:当x<0或1<x<3时,y1>y2.
(3)

由y1=-x+4可得点E的坐标为(4,0),
则S△AOE=
 OE×A纵=6,S△BOE=
OE×A纵=6,S△BOE= OE×B纵=2,
OE×B纵=2,故可得S△AOB=S△AOE-S△BOE=4;
(4)设点P的坐标为(x,
 ),
),S△MPO=
 OM×P横=x,S△POQ=
OM×P横=x,S△POQ= |a|=
|a|= ,S△MON=
,S△MON= OM×ON=2,
OM×ON=2,则S△MOP+S△OPQ=S△MON+S四边形MNQP=S四边形MPQO,
即x+
 =2+2,
=2+2,解得:x=
 ,则
,则 =
= ,
,故点P的坐标为:(
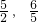 ).
).分析:(1)将点A(1,3),代入y1、y2可得出k、a的值,然后将点B(m,1)代入y2可得出m的值.
(2)根据图象即可得出y1>y2时x的取值范围.
(3)求出直线AB与x轴的交点E的坐标,然后求出S△AOE、S△BOE,根据S△AOB=S△AOE-S△BOE,可得出△AOB的面积.
(4)根据(1)中求得a的值,可设点P(x,
 ),连接OP,根据S△MOP+S△OPQ=S△MON+S四边形MNQP,可得出x的值,继而得出点P的坐标.
),连接OP,根据S△MOP+S△OPQ=S△MON+S四边形MNQP,可得出x的值,继而得出点P的坐标.点评:本题考查了反比例函数综合题,涉及了待定系数法求函数解析式、不规则图形面积的求法及反比例函数k的几何意义,综合性较强,解答本题要求我们熟悉各个知识点,能将所学的知识融会贯通,难度较大.

练习册系列答案
相关题目