题目内容
将一直径为34cm的圆形纸片(图甲)剪成如图乙所示的纸片,再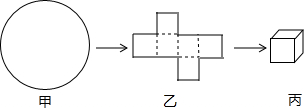 将纸片沿虚线折叠得到正方体(图丙)形状的纸盒,则这样的纸盒体积最大为
将纸片沿虚线折叠得到正方体(图丙)形状的纸盒,则这样的纸盒体积最大为
 将纸片沿虚线折叠得到正方体(图丙)形状的纸盒,则这样的纸盒体积最大为
将纸片沿虚线折叠得到正方体(图丙)形状的纸盒,则这样的纸盒体积最大为136
| 17 |
136
cm3.| 17 |
分析:要求这样的纸盒的最大体积,只需求得它的最大棱长.把正方体的表面展开图放到圆中,根据勾股定理进行计算即可.
解答: 解:如图所示.设正方体的棱长是acm.
解:如图所示.设正方体的棱长是acm.
在Rt△AOB中,OA=17cm,AB=2a,OB=
,根据勾股定理,得
+4a2=172,
解得a=±2
(负值舍去).
则这样的纸盒体积最大为(2
)3=136
cm3.
故答案为:136
.
 解:如图所示.设正方体的棱长是acm.
解:如图所示.设正方体的棱长是acm.在Rt△AOB中,OA=17cm,AB=2a,OB=
| a |
| 2 |
| a2 |
| 4 |
解得a=±2
| 17 |
则这样的纸盒体积最大为(2
| 17 |
| 17 |
故答案为:136
| 17 |
点评:本题主要考查了正方形的性质及垂径定理等知识点,本题中根据垂径定理求出小正方形的边长是解题的关键.

练习册系列答案
相关题目
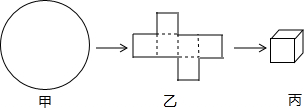 将纸片沿虚线折叠得到正方体(图丙)形状的纸盒,则这样的纸盒体积最大为________ cm3.
将纸片沿虚线折叠得到正方体(图丙)形状的纸盒,则这样的纸盒体积最大为________ cm3.