Question

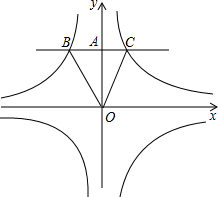（2012•常州）如图，已知反比例函数y=

k1

x

（k₁＞0），y=

k2

x

（k₂＜0）．点A在y轴的正半轴上，过点A作直线BC∥x轴，且分别与两个反比例函数的图象交于点B和C，连接OC、OB．若△BOC的面积为

5

2

，AC：AB=2：3，则k₁=

2

，k₂=

-3

．

Answer 1

分析：根据反比例函数系数的几何意义可得，|k₁|+|k₂|的值以及|k₁|：|k₂|的值，然后联立方程组求解得到|k₁|与|k₂|的值，然后即可得解．

解答：解：∵△BOC的面积为

5

2

，
∴

1

2

|k₁|+

1

2

|k₂|=

5

2

，
即|k₁|+|k₂|=5①，
∵AC：AB=2：3，
∴|k₁|：|k₂|=2：3②，
①②联立

|k1|+|k2|=5 |k1|：|k2|=2：3

，
解得|k₁|=2，|k₂|=3，
∵k₁＞0，k₂＜0，
∴k₁=2，k₂=-3．
故答案为：2，-3．

点评：本题考查了反比例函数系数的几何意义，过双曲线上的任意一点分别向两条坐标作垂线，与坐标轴围成的矩形面积就等于|k|，根据题意得到两个关于反比例函数系数的方程是解题的关键．