题目内容
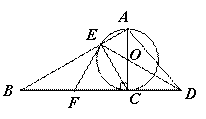
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC 的延长线于点D,点F为BC的中点,连接EF
的延长线于点D,点F为BC的中点,连接EF
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
 |
 |
证明:(1)连接FO
易证OF∥AB
∵AC⊙O的直径
∴CE⊥AE
∵OF∥AB
∴OF⊥CE
∴OF所在直线垂直平分CE
∴FC=FE,OE=OC
∴∠FEC=∠FCE,∠0EC=∠0CE
∵Rt△ABC
∴∠ACB=90°
即:∠0CE+∠FCE=90°
∴∠0EC+∠FEC=90°
即:∠FEO=90°
∴FE为⊙O的切线
 |
(2)
∵⊙O的半径为3
∴AO=CO=EO=3
∵∠EAC=60°,OA=OE
∴∠EOA=60°
∴∠COD=∠EOA=60°
∵在Rt△OCD中,∠COD=60°,OC=3
∴CD=
∵在Rt△ACD中,∠ACD=90°,
CD= ,AC=6
,AC=6
∴AD=

练习册系列答案
相关题目
下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差
与方差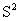 :
:
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 561 | 560 | 561 | 560 |
| 方差 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择
A. 甲 B.乙 C.丙 D.丁
 的根,则该三角形的周长是( )
的根,则该三角形的周长是( ) .
. 化简,再求值,其中
化简,再求值,其中
 ,
, ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定 ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
