Question

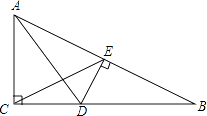
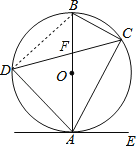
【题目】如图，已知AB是⊙O的直径，弦CD与直径AB相交于点F．点E在⊙O外，做直线AE，且∠EAC=∠D．

（1）求证：直线AE是⊙O的切线．

（2）若∠BAC=30°，BC=4，cos∠BAD=，CF=，求BF的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）由直径所对的圆周角是直角得：∠ADB=90°，则∠ADC+∠CDB=90°，所以∠EAC+∠BAC=90°，则直线AE是⊙O的切线；

（2）分别计算AC和BD的长，证明△DFB∽△AFC，列比例式得：，得出结论．

试题解析：（1）连接BD，∵AB是⊙O的直径，∴∠ADB=90°，即∠ADC+∠CDB=90°，∵∠EAC=∠ADC，∠CDB=∠BAC，∴∠EAC+∠BAC=90°，即∠BAE=90°，∴直线AE是⊙O的切线；

（2）∵AB是⊙O的直径，∴∠ACB=90°，Rt△ACB中，∠BAC=30°，∴AB=2BC=2×4=8，由勾股定理得：AC==，Rt△ADB中，cos∠BAD==，∴=，∴AD=6，∴BD= =，∵∠BDC=∠BAC，∠DFB=∠AFC，∴△DFB∽△AFC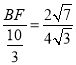，∴，∴，∴BF=．