Question

将两枚相同大小的1圆硬币A、B紧贴在一起，硬币A固定不动，硬币B的边缘紧贴硬币A并围绕硬币A旋转．当硬币B围绕硬币A旋转一周回到原来位置时，它围绕着自己的中心旋转的角度是360度的

2

倍．

Answer 1

分析：设⊙A，⊙B的半径为R，由⊙B绕⊙A旋转一周回到原来位置，说明B绕A旋转一周，它的路径为2π•2R=4πR，得到⊙B转动了4πR÷2πR=2周，即可得到答案．

解答：解：如图，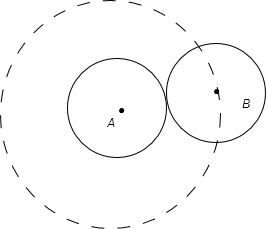
设⊙A，⊙B的半径为R，
∵⊙B绕⊙A旋转一周回到原来位置，
∴B绕A旋转一周，它的路径为2π•2R=4πR，
∴⊙B转动了4πR÷2πR=2周，
即它围绕着自己的中心旋转的角度是360度的2倍．
故答案为：2．

点评：本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．也考查了圆的周长公式．