Question

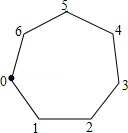
如图，一枚棋子放在七角棋盘的第0号角，现依逆时针方向移动这枚棋子，其各步依次移动1，2，3，…，n个角，如第一步从0号角移动到第1号角，第二步从第1号角移动到第3号角，第三步从第3号角移动到第6号角，…．若这枚棋子不停地移动下去，则这枚棋子永远不能到达的角的个数是(   )

A．0

B．1

C．2

D．3

Answer 1

D

试题分析：因棋子移动了k次后走过的总格数是1+2+3+…+k=k（k+1），然后根据题目中所给的第k次依次移动k个顶点的规则，可得到不等式最后求得解．
因棋子移动了k次后走过的总格数是1+2+3+…+k=k（k+1），应停在第k（k+1）-7p格，
这时P是整数，且使0≤k（k+1）-7p≤6，分别取k=1，2，3，4，5，6，7时，
k（k+1）-7p=1，3，6，3，1，0，0，发现第2，4，5格没有停棋，
若7＜k≤10，设k=7+t（t=1，2，3）代入可得，k（k+1）-7p=7m+t（t+1），
由此可知，停棋的情形与k=t时相同，
故第2，4，5格没有停棋，
即这枚棋子永远不能到达的角的个数是3．
故选D．
点评：解题的关键是知道棋子所停的规则，找到规律，然后得到不等式求解．