题目内容
解方程组:
解:由①得:3y=2x-5,
∴
由②得: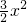 -3y=
-3y= ,
,
把 代入得:3x2-4x+1=0,
代入得:3x2-4x+1=0,
∴x1= ,x2=1,
,x2=1,
分别代入方程①得y1=-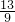 ,y2=-1,
,y2=-1,
所以原方程组的解为: ,
, .
.
分析:首先把方程①变为 ,然后代入方程②中即可消去y,然后解关于x的一元二次方程即可求出x,再代入方程①求出y,这样就求出的方程组的解.
,然后代入方程②中即可消去y,然后解关于x的一元二次方程即可求出x,再代入方程①求出y,这样就求出的方程组的解.
点评:此题主要考查了解高次方程组,解题的基本方法计算消元和降次,消元的基本方法是代入消元和加减消元,降次的基本方法也代入法和加减法.
∴

由②得:
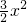 -3y=
-3y= ,
,把
 代入得:3x2-4x+1=0,
代入得:3x2-4x+1=0,∴x1=
 ,x2=1,
,x2=1,分别代入方程①得y1=-
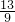 ,y2=-1,
,y2=-1,所以原方程组的解为:
 ,
, .
.分析:首先把方程①变为
 ,然后代入方程②中即可消去y,然后解关于x的一元二次方程即可求出x,再代入方程①求出y,这样就求出的方程组的解.
,然后代入方程②中即可消去y,然后解关于x的一元二次方程即可求出x,再代入方程①求出y,这样就求出的方程组的解.点评:此题主要考查了解高次方程组,解题的基本方法计算消元和降次,消元的基本方法是代入消元和加减消元,降次的基本方法也代入法和加减法.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 (1)解方程组:
(1)解方程组: