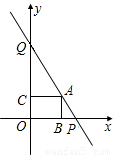题目内容
如图,A、B两点在反比例函数 (x>0)的图象上.
(x>0)的图象上.(1)求该反比例函数的解析式;
(2)连接AO、BO和AB,请直接写出△AOB的面积.

【答案】分析:(1)利用待定系数法直接把A(1,6)反比例函数的 (x>0)即可算出k的值,进而得到反比例函数解析式;
(x>0)即可算出k的值,进而得到反比例函数解析式;
(2)首先求出直线AB的解析式,再算出C、D两点坐标,进而可得到△AOC,△BOD,△COD的面积,再利用△COD的面积-△AOC的面积-△BOD的面积即可得到答案.
解答: 解:(1)∵点A(1,6)在反比例函数的
解:(1)∵点A(1,6)在反比例函数的 (x>0)图象上,
(x>0)图象上,
∴k=1×6=6,
∴反比例函数解析式为y= (x>0);
(x>0);
(2)∵A、B两点在反比例函数y= 的图象上,
的图象上,
过A、B画直线交x轴于D点,交y轴于C点,
设直线AB的解析式为y=kx+b,
∵图象经过A(1,6),B(6,1),
∴ ,
,
解得 ,
,
∴直线AB的解析式为y=-x+7,
∴C(0,7),D(7,0),
∴S△AOC= ×7×1=3.5
×7×1=3.5
S△BOD= ×7×1=3.5,
×7×1=3.5,
S△COD= ×7×7=24.5,
×7×7=24.5,
∴△AOB的面积是:24.5-3.5×2=17.5.
点评:此题主要考查了待定系数法求反比例函数解析式,以及一次函数解析式,解决问题的关键是求出△AOC,△BOD,△COD的面积.
 (x>0)即可算出k的值,进而得到反比例函数解析式;
(x>0)即可算出k的值,进而得到反比例函数解析式;(2)首先求出直线AB的解析式,再算出C、D两点坐标,进而可得到△AOC,△BOD,△COD的面积,再利用△COD的面积-△AOC的面积-△BOD的面积即可得到答案.
解答:
 解:(1)∵点A(1,6)在反比例函数的
解:(1)∵点A(1,6)在反比例函数的 (x>0)图象上,
(x>0)图象上,∴k=1×6=6,
∴反比例函数解析式为y=
 (x>0);
(x>0);(2)∵A、B两点在反比例函数y=
 的图象上,
的图象上,过A、B画直线交x轴于D点,交y轴于C点,
设直线AB的解析式为y=kx+b,
∵图象经过A(1,6),B(6,1),
∴
 ,
,解得
 ,
,∴直线AB的解析式为y=-x+7,
∴C(0,7),D(7,0),
∴S△AOC=
 ×7×1=3.5
×7×1=3.5S△BOD=
 ×7×1=3.5,
×7×1=3.5,S△COD=
 ×7×7=24.5,
×7×7=24.5,∴△AOB的面积是:24.5-3.5×2=17.5.
点评:此题主要考查了待定系数法求反比例函数解析式,以及一次函数解析式,解决问题的关键是求出△AOC,△BOD,△COD的面积.

练习册系列答案
相关题目

 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.