题目内容
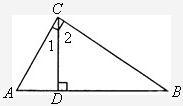
如图,△ABC≌△FED,∠C=∠EDF=90°,点E在AB边上,点C、D、B、F在同一条直线上,AC=4,AB=5.则△BDE与△BCA的面积比 .
【答案】分析:欲求面积比,可考虑在相似三角形中用相似三角形的性质面积比等于对应边的比的平方来求.
解答:解:易知△BDE与△BCA相似,已知AC=4,AB=5,
由勾股定理知,BC=3;
又△ABC≌△FED,即ED=BC=3,故DE:CA=3:4,
则△BDE与△BCA的面积比=( )2=(
)2=( )2=
)2= .
.
点评:本题关键是要懂得找相似三角形,利用相似三角形的性质求解.
解答:解:易知△BDE与△BCA相似,已知AC=4,AB=5,
由勾股定理知,BC=3;
又△ABC≌△FED,即ED=BC=3,故DE:CA=3:4,
则△BDE与△BCA的面积比=(
 )2=(
)2=( )2=
)2= .
.点评:本题关键是要懂得找相似三角形,利用相似三角形的性质求解.

练习册系列答案
相关题目
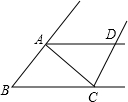 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 ,且CB=CE.
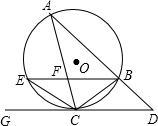
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.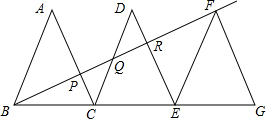 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且