Question

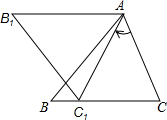在△ABC中，AB=BC，∠C＞60°，将△ABC绕点A沿顺时针方向旋转得到△AB₁C₁，使点C₁落在线段BC上（点C₁与点C不重合），请猜想边AB₁与边CB有什么关系，并说明理由．

Answer 1

解：AB₁=CB，且AB₁∥CB，
理由如下：∵△ABC绕点A沿顺时针方向旋转得到△AB₁C₁，
∴AB₁=AB=CB，且AC₁=AC，∠B₁AC₁=∠BAC，
∵AB=BC，
∴∠BAC=∠C，
∴∠B₁AC₁=∠C，
∵AC=AC₁，
∴∠AC₁C=∠C，
∴∠B₁AC₁=∠AC₁C，
∴AB₁∥CB．
所以AB₁=CB，且AB₁∥CB．
分析：由于是将△ABC绕点A沿顺时针方向旋转得到△AB₁C₁，所以AB₁=AB=CB，AC=AC₁，所以∠AC₁C=∠ACC₁，又因为∠B₁AC₁=∠B₁C₁A=∠ACB，所以∠B₁AC₁=∠AC₁C，所以AB₁∥CB．
点评：本题结合旋转知识，考查了平行线的判定：内错角相等，两直线平行．