题目内容
直角三角形的两直角边的比为3：4，斜边长为25，则斜边上的高为（ ）
A、
| ||
B、
| ||
| C、12 | ||
| D、15 |
分析：根据勾股定理以及两直角边的比为3：4，可知斜边是5份．又斜边的长是25，所以一份是5．即两条直角边的长分别是15、20．再根据斜边上的高等于两条直角边的乘积除以斜边，得斜边上的高是12．
解答：解：设两直角边长为3x、4x，根据勾股定理知斜边长为5x．
又斜边长为25，所以x=5，
即两直角边为15、20，
假设斜边上的高为h，则15×20=25h，
解之得h=12，
故选C．
又斜边长为25，所以x=5，
即两直角边为15、20，
假设斜边上的高为h，则15×20=25h，
解之得h=12，
故选C．
点评：能够根据已知条件结合勾股定理求出直角三角形的三边．特别注意结论：直角三角形斜边上的高等于两条直角边的乘积除以斜边．此结论在计算中运用可以简便计算．
练习册系列答案
相关题目
，
表示直角三角形的两直角边（
），下列四个说法：
，②
，③
，④
.
，
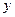表示直角三角形的两直角边（
），下列四个说法：①
，②
，③
，④
.其中说法正确的是 ……………………【 】
，
表示直角三角形的两直角边（
），下列四个说法：
，②
，③
，④
.